【解説】【MQL5 community】 Fourier Extrapolator of Price : ここでは、multi-harmonic (or multi-tone) trigonometric model を用いて、次のように価格の変化を捉える.
x[i] = m + Sum( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
where:
■x[i] - past price at i-th bar, total n past prices
■m - bias
■a[h] and b[h] - scaling coefficients of harmonics
■w[h] - frequency of a harmonic
■h - harmonic number
■H - total number of fitted harmonics
特にここでは、Quinn-Fernandesのアルゴリズムを使用する。
(注)フーリエ解析では、周期は2*pi*h/nであったが、ここではn周期。
【シグナル】
移動平均と同様に使用でき、 ラインを上抜けしたら、「買い」、下抜けしたら「売り」。 上昇基調になりそうな(移動平均が右肩上がり)場合のトレンドを把握することができる。
//+--------------------------------------------------------------------------------------+
//| Fourier_Extrapolator_of_Price.mq5 |
//| Copyright 2010, gpwr |
//+--------------------------------------------------------------------------------------+
#property copyright "gpwr"
#property version "1.00"
#property description "Extrapolation of open prices by trigonometric (multitone) model"
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots 2
//--- future model outputs
#property indicator_label1 "Modeled future"
#property indicator_type1 DRAW_LINE
#property indicator_color1 Red
#property indicator_style1 STYLE_SOLID
#property indicator_width1 1
//--- past model outputs
#property indicator_label2 "Modeled past"
#property indicator_type2 DRAW_LINE
#property indicator_color2 Blue
#property indicator_style2 STYLE_SOLID
#property indicator_width2 1
//Global constants
#define pi 3.141592653589793238462643383279502884197169399375105820974944592
//===================================== INPUTS ===========================================
input int Npast =300; // # of past bars, to which trigonometric series is fitted
input int Nfut =50; // # of predicted future bars
input int Nharm =20; // # of harmonics in model
input double FreqTOL =0.00001; // Tolerance of frequency calculations
// Global variables
int N;
// Indicator buffers
double ym[],xm[];
// Custom indicator initialization function ---------------------------------------------+
void OnInit()
{
// Initialize global variables
N=MathMax(Npast,Nfut+1);
// Map indicator buffers
ArraySetAsSeries(xm,true);
ArraySetAsSeries(ym,true);
SetIndexBuffer(0,ym,INDICATOR_DATA);
SetIndexBuffer(1,xm,INDICATOR_DATA);
IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
IndicatorSetString(INDICATOR_SHORTNAME,"Fourier("+string(Npast)+")");
PlotIndexSetInteger(0,PLOT_SHIFT,Nfut);
}
//====================================== MAIN ============================================
int OnCalculate(const int rates_total,
const int prev_calculated,
const datetime& Time[],
const double& Open[],
const double& High[],
const double& Low[],
const double& Close[],
const long& tick_volume[],
const long& volume[],
const int& spread[])
{
// Check for insufficient data
if(rates_total<Npast)
{
Print("Error: not enough bars in history!");
return(0);
}
// Initialize indicator buffers to EMPTY_VALUE
ArrayInitialize(xm,EMPTY_VALUE);
ArrayInitialize(ym,EMPTY_VALUE);
// Make all prices available
MqlRates rates[];
ArraySetAsSeries(rates,true);
if(CopyRates(NULL,0,0,Npast,rates)<=0) return(0);
// Main cycle ---------------------------------------------------------------------------+
// Prepare input data
double x[];
ArrayResize(x,Npast);
double av=0;
for(int i=0;i<Npast;i++)
{
x[i]=rates[i].open;
av+=x[i];
}
av/=Npast;
// Initialize model outputs
for(int i=0;i<N;i++)
{
xm[i]=av;
if(i<=Nfut) ym[i]=av;
}
// Fit trigonometric model and calculate predictions
for(int harm=1;harm<=Nharm;harm++)
{
double w,m,a,b;
Freq(x,Npast,w,m,a,b);
for(int i=0;i<N;i++)
{
xm[i]+=m+a*MathCos(w*i)+b*MathSin(w*i);
if(i<=Nfut) ym[Nfut-i]+=m+a*MathCos(w*i)-b*MathSin(w*i);
}
}
return(rates_total);
}
//==================================== FUNCTIONS =========================================
// Quinn and Fernandes algorithm for finding frequency ----------------------------------+
void Freq(double& x[],int n,double& w,double& m,double& a,double& b)
{
double z[];
ArrayResize(z,n);
double alpha=0.0;
double beta=2.0;
z[0]=x[0]-xm[0];
while(MathAbs(alpha-beta)>FreqTOL)
{
alpha=beta;
z[1]=x[1]-xm[1]+alpha*z[0];
double num=z[0]*z[1];
double den=z[0]*z[0];
for(int i=2;i<n;i++)
{
z[i]=x[i]-xm[i]+alpha*z[i-1]-z[i-2];
num+=z[i-1]*(z[i]+z[i-2]);
den+=z[i-1]*z[i-1];
}
beta=num/den;
}
w=MathArccos(beta/2.0);
TrigFit(x,n,w,m,a,b);
}
// Least-squares fitting of trigonometric series ----------------------------------------+
void TrigFit(double& x[],int n,double w,double& m,double& a,double& b)
{
double Sc =0.0;
double Ss =0.0;
double Scc=0.0;
double Sss=0.0;
double Scs=0.0;
double Sx =0.0;
double Sxc=0.0;
double Sxs=0.0;
for(int i=0;i<n;i++)
{
double c=MathCos(w*i);
double s=MathSin(w*i);
double dx=x[i]-xm[i];
Sc +=c;
Ss +=s;
Scc+=c*c;
Sss+=s*s;
Scs+=c*s;
Sx +=dx;
Sxc+=dx*c;
Sxs+=dx*s;
}
Sc /=n;
Ss /=n;
Scc/=n;
Sss/=n;
Scs/=n;
Sx /=n;
Sxc/=n;
Sxs/=n;
if(w==0.0)
{
m=Sx;
a=0.0;
b=0.0;
}
else
{
// calculating a, b, and m
double den=MathPow(Scs-Sc*Ss,2)-(Scc-Sc*Sc)*(Sss-Ss*Ss);
a=((Sxs-Sx*Ss)*(Scs-Sc*Ss)-(Sxc-Sx*Sc)*(Sss-Ss*Ss))/den;
b=((Sxc-Sx*Sc)*(Scs-Sc*Ss)-(Sxs-Sx*Ss)*(Scc-Sc*Sc))/den;
m=Sx-a*Sc-b*Ss;
}
}
【表示結果】
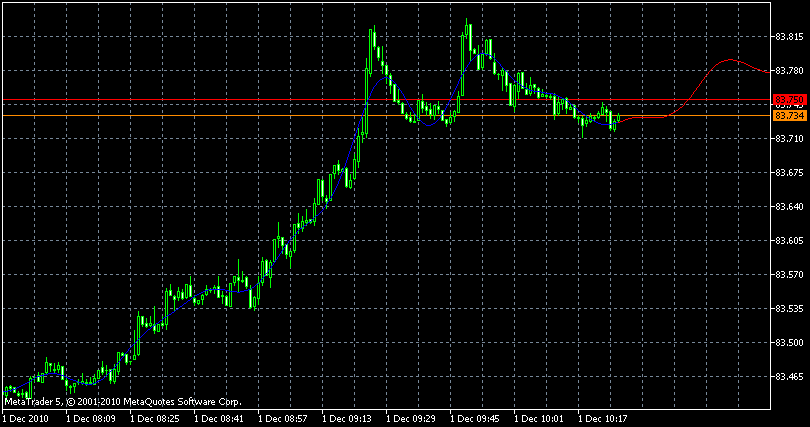
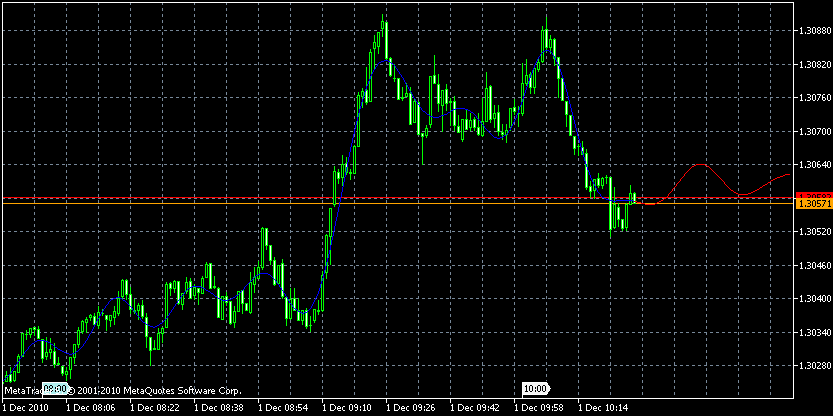
Back to Meta Trader