【解説】【MQL5 community】 Hodrick-Prescott_Filter : Hodrick-PrescottフィルターはRBCモデル(マクロ経済学)で使われ、長期トレンドを除去し、最近のトレンドをに見出す手法。
【計算法】
Σ_{t=1}^T (y_t-s_t)^2+λ Σ_{t=2}^{T-1} {(s_{t+1}-s_t)-(s_t-s_{t-1})}^2
第1項目は実データとトレンドの乖離、2項目はトレンド間の 変化幅を表し、1項目と2項目の和を最小化するようにs(トレンド) を選ぶ。また、λによりトレンドの滑らかさを調整することが できる(月次データではλ≠14400が推奨されている)。 (Hodrick, R. J. and E.C. Prescott. "Postwar U.S. Business Cycles: An Empirical Investigation," Journal of Money, Credit, and Banking, 29, 1-16 (1997))
実際のデータにこれを使用するのか、対数変換したものを使用するのかが議論があるようです。ちなみにRBCでは対数変換したものを基本的に使用するようです。
【シグナル】
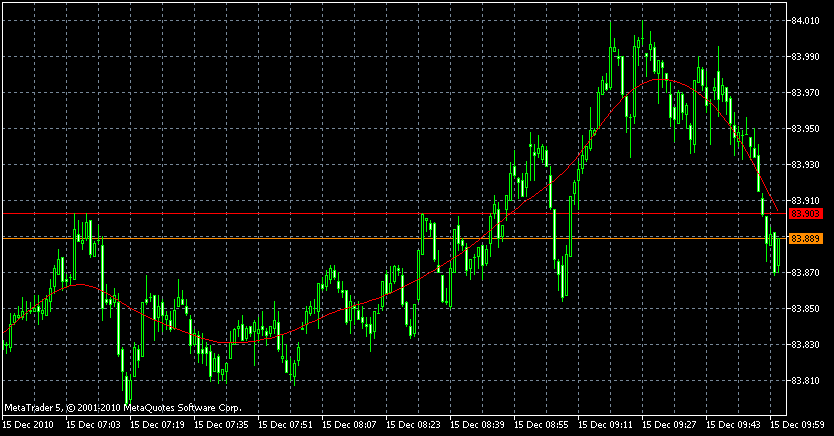
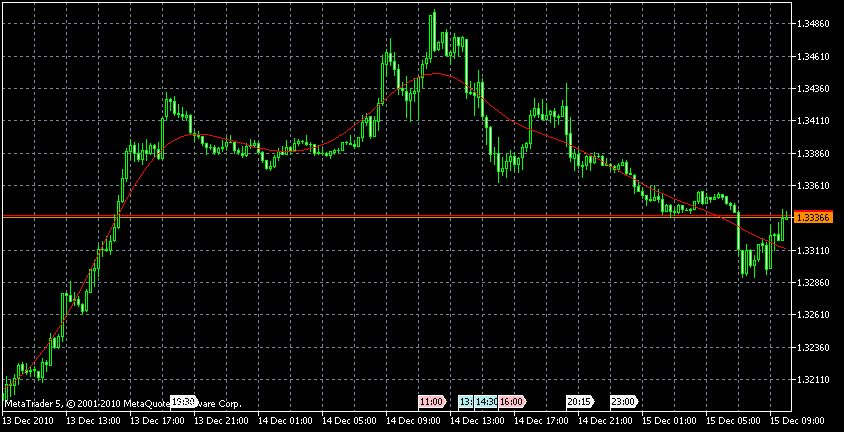
移動平均 と同様に、移動平均のラインを上抜けしたら、「買い」、下抜けしたら「売り」。 上昇基調になりそうな(移動平均が右肩上がり)場合のトレンドを把握することができる。
//+--------------------------------------------------------------------------------------+
//| Hodrick-Prescott Filter.mq5 |
//| Copyright 2010, gpwr |
//| vlad1004@yahoo.com |
//+--------------------------------------------------------------------------------------+
#property copyright "gpwr"
#property version "1.00"
#property description "Hodrick-Prescott Filter"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_plots 1
#property indicator_label1 "filter"
#property indicator_type1 DRAW_LINE
#property indicator_color1 Red
#property indicator_style1 STYLE_SOLID
#property indicator_width1 1
//===================================== INPUTS ===========================================
input int Per =50; // HP filter period
input int N =500; // # of prices to smooth
// Global variables
int PrevBars;
double Lambda;
// Indicator buffers
double hpf[];
// Custom indicator initialization function ---------------------------------------------+
void OnInit()
{
// Initialize global variables
PrevBars=Bars(_Symbol,_Period)-1;
Lambda=0.0625/MathPow(MathSin(M_PI/Per),4);
// Map indicator buffers
ArraySetAsSeries(hpf,true);
SetIndexBuffer(0,hpf,INDICATOR_DATA);
IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
IndicatorSetString(INDICATOR_SHORTNAME,"HPF("+string(Per)+")");
}
//====================================== MAIN ============================================
int OnCalculate(const int bars,
const int prev_calculated,
const datetime& Time[],
const double& Open[],
const double& High[],
const double& Low[],
const double& Close[],
const long& tick_volume[],
const long& volume[],
const int& spread[])
{
// Check for insufficient data and new bar
if(bars<N)
{
Print("Error: not enough bars in history!");
return(0);
}
if(PrevBars==bars) return(bars);
PrevBars=bars;
// Initialize indicator buffer to EMPTY_VALUE
ArrayInitialize(hpf,EMPTY_VALUE);
// Reverse indexing direction for Open
ArraySetAsSeries(Open,true);
// Main cycle ---------------------------------------------------------------------------+
for(int i=0;i<N;i++) hpf[i]=Open[i];
HPF(N,Lambda,hpf);
return(bars);
}
//==================================== FUNCTIONS =========================================
// Hodrick-Prescott Filter---------------------------------------------------------------+
void HPF(int n,double lambda,double& x[])
{
double a[],b[],c[],h1,h2,h3,h4,h5,hh1,hh2,hh3,hh5,hb,hc,z;
ArrayResize(a,n);
ArrayResize(b,n);
ArrayResize(c,n);
a[0]=1.0+lambda;
b[0]=-2.0*lambda;
c[0]=lambda;
for(int i=1;i<n-2;i++)
{
a[i]=6.0*lambda+1.0;
b[i]=-4.0*lambda;
c[i]=lambda;
}
a[1]=5.0*lambda+1;
a[n-1]=1.0+lambda;
a[n-2]=5.0*lambda+1.0;
b[n-2]=-2.0*lambda;
b[n-1]=0.0;
c[n-2]=0.0;
c[n-1]=0.0;
//Forward
for(int i=0;i<n;i++)
{
z=a[i]-h4*h1-hh5*hh2;
hb=b[i];
hh1=h1;
h1=(hb-h4*h2)/z;
b[i]=h1;
hc=c[i];
hh2=h2;
h2=hc/z;
c[i]=h2;
a[i]=(x[i]-hh3*hh5-h3*h4)/z;
hh3=h3;
h3=a[i];
h4=hb-h5*hh1;
hh5=h5;
h5=hc;
}
//Backward
h2=0;
h1=a[n-1];
x[n-1]=h1;
for(int i=n-2;i>=0;i--)
{
x[i]=a[i]-b[i]*h1-c[i]*h2;
h2=h1;
h1=x[i];
}
}
【表示結果】
Back to Meta Trader