Replicator Equation

/*

The Ultimatum Minigame (Vega-Redondo (1996), p.114, Samuelson (1997), Ch.5.)

dot{y} = y(1-y)(3x-1)
dot{x} = x(1-x)(y-1)

runge-kutta method 

y1=y (0<=y1<=1)
y2=x (0<=y2<=1)

初期値はランダムに。60個
*/

#include 
#include 

#define h 0.01 /*h*/

#define IA 16807
#define IM 2147483647
#define AM (1.0/IM)
#define IQ 127773
#define IR 2836
#define MASK 123459876

unsigned long int idum = 1024;

float ran0(long *);

double FUNC1();
double FUNC2();

main()
{
  int i,j; /*j; step number*/
  double I1[62][10002],I2[62][10002];

/*Initial Condition*/
   for(i=1;i<=60;i++) {
         I1[i][1]=ran0(&idum);
         I2[i][1]=ran0(&idum);
   }

  double nt=0.0,t=0.0;
  double k11=0.0,k12=0.0,k21=0.0,k22=0.0,
    k31=0.0,k32=0.0,k41=0.0,k42=0.0;

  for(i=1; i<=60;i++)
    {
     for(j=1; j<=10000;j++)
     {
      k11=h*FUNC1(t,I1[i][j],I2[i][j]);
      k12=h*FUNC2(t,I1[i][j],I2[i][j]);
      k21=h*FUNC1(t+0.5*h,I1[i][j]+0.5*k11,I2[i][j]+0.5*k12);
      k22=h*FUNC2(t+0.5*h,I1[i][j]+0.5*k11,I2[i][j]+0.5*k12);
      k31=h*FUNC1(t+0.5*h,I1[i][j]+0.5*k21,I2[i][j]+0.5*k22);
      k32=h*FUNC2(t+0.5*h,I1[i][j]+0.5*k21,I2[i][j]+0.5*k22);
      k41=h*FUNC1(t+h,I1[i][j]+k31,I2[i][j]+k32);
      k42=h*FUNC2(t+h,I1[i][j]+k31,I2[i][j]+k32);
     
      I1[i][j+1]=I1[i][j]+0.166666667*(k11+2.0*k21+2.0*k31+k41);
      I2[i][j+1]=I2[i][j]+0.166666667*(k12+2.0*k22+2.0*k32+k42);

      nt=t+h;

      /*printf("%f %f \n",I1[i][j],I2[i][j]);*/

      I1[i][j]=I1[i][j+1];
      I2[i][j]=I2[i][j+1];
      t=nt;
     }
   }

  for(i=1; i<=60;i++)
    {
     for(j=1; j<=10000;j++)
     {
      printf("%f %f \n",I1[i][j],I2[i][j]);
     }
      printf("\n");
   }

  return 0;
}

/*y=y1,x=y2*/
double FUNC1(double t, double y1, double y2)
{
  return ( y1*(1.0-y1)*(3.0*y2-1.0));
}

/**/
double FUNC2(double t, double y1, double y2)
{
  return ( y2*(1.0-y2)*(y1-1.0) );
}

float ran0(long *idum)
{
  long k;
  float ans;
  
  *idum ^= MASK;
  k=(*idum)/IQ;
  *idum=IA*(*idum-k*IQ)-IR*k;
  if (*idum < 0) *idum += IM;
  ans=AM*(*idum);
  *idum ^= MASK;
  return ans;
}
出力結果
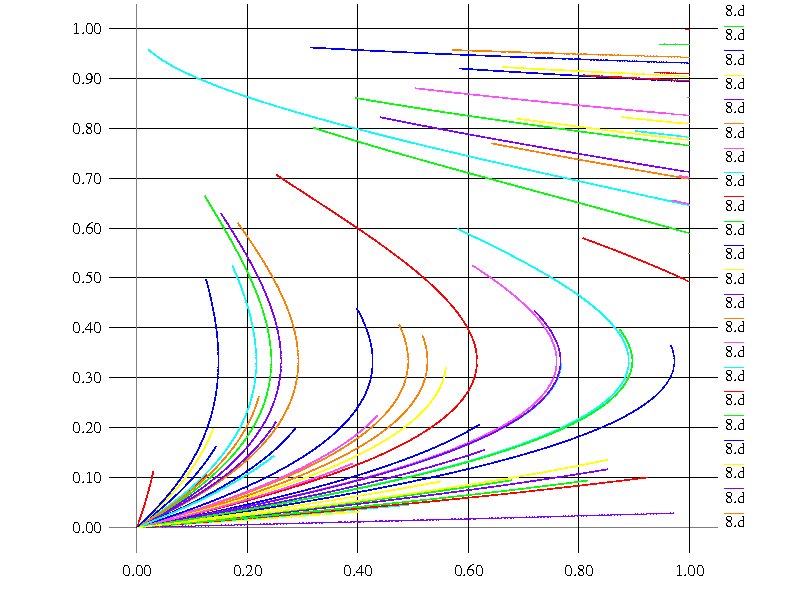
The Ultimatum Minigame (Samuelson (1997), Ch.5, Vega-Redondo (1996), p.114.)

Back to C Language