Logistic

/*
Logistic Equation

dot{n} = r*(1.0-n/K)*n

*/

#include 
#include 
#include 

#define T_END 1000
#define r 0.1
#define K 50.0
#define h 0.1  /*h 分割数*/

double FUNC(); /* 関数の例*/

main()
{
  int j; /*j;step number*/
  double nn=0.0, n=100.0;
  double nt=0.0,t=0.0;
  double k1=0.0, k2=0.0,k3=0.0,k4=0.0;
  
  for(j=0;j<=T_END;j++)
    {
      k1 = h*FUNC(t,n);
      k2 = h*FUNC(t+0.5*h,n+0.5*k1);
      k3 = h*FUNC(t+0.5*h,n+0.5*k2);
      k4 = h*FUNC(t+h,n+k3);

      nn = n + 0.16666667*(k1+2.0*k2+2.0*k3+k4);
      nt = t + h;
 
      printf("%d %f\n",j,n);
      n = nn;
      t = nt;
    }
  return 0;
}

/*関数の例*/
double FUNC(double t, double n)
{
  return (r*(1.0-n/K)*n);
}

出力結果

この微分方程式には解析解が存在し、それに収束する。しかし離散時間体系にすると、次のような変なことが起こる。

/*
離散時間体系：

x_{n+1}=a*(1.0-x)*x
*/

#include 
#include 
#include 

#define a 4.0

main()
{
  int j; /*j;step number*/
  double x=0.1,nx=0.0;

  for(j=0;j<=100;j++)
    {
	nx=a*(1.0-x)*x;
	printf("%f %f\n",nx, x);
	/*printf("%d %f\n",j, nx);*/
    x=nx;
    }
  return 0;
}

出力結果

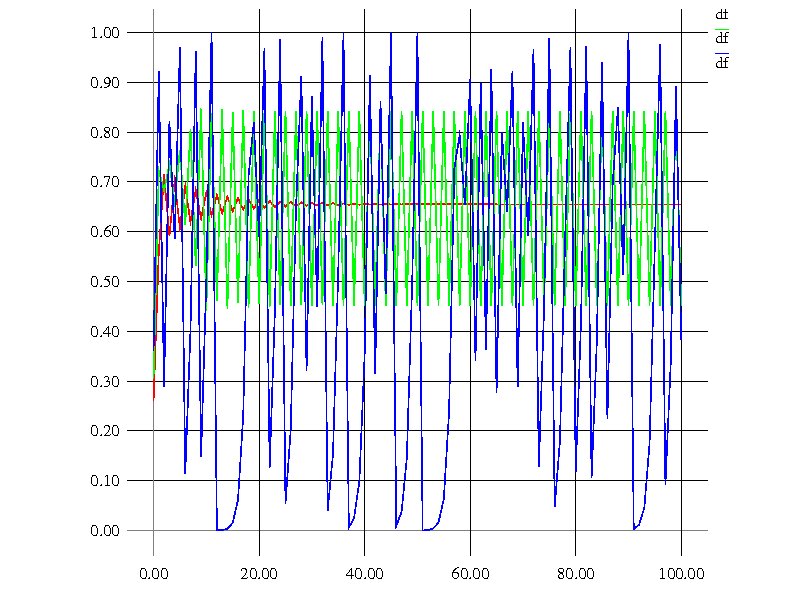
TIME EVOLUTION(aの値によって、収束(a=2.9)、周期的(a=3.4)、一見ランダム(a=4.0)なように)

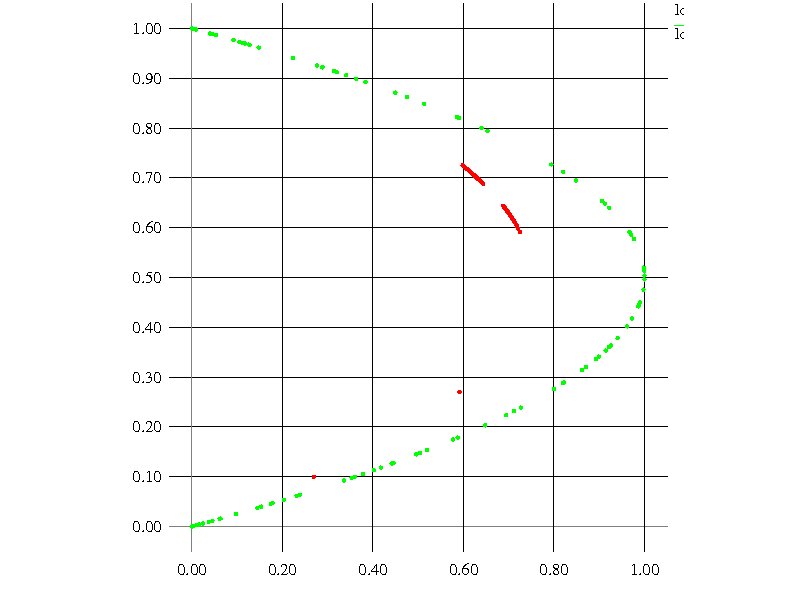
NXとX(RED: a=3.0, GREEN: a=4.0) 特にa=4の場合、時間発展は一見ランダムのようでしたが、規則性が存在するということが分かります。

/*
Logistic Map

OUTPUT Command
./a.out | xgrpah -nl -p

*/
#include 
#include 

main(void)
{
  double nx,c;
  double x=0.65;

  for(c = 2.9 ; c <= 4.0; c += 0.00001)
    {
      nx = c*x*(1. - x );
      printf("%f  %f\n", c , nx );
      x = fmod( nx ,1.);
    }
  return 0;
}

出力結果

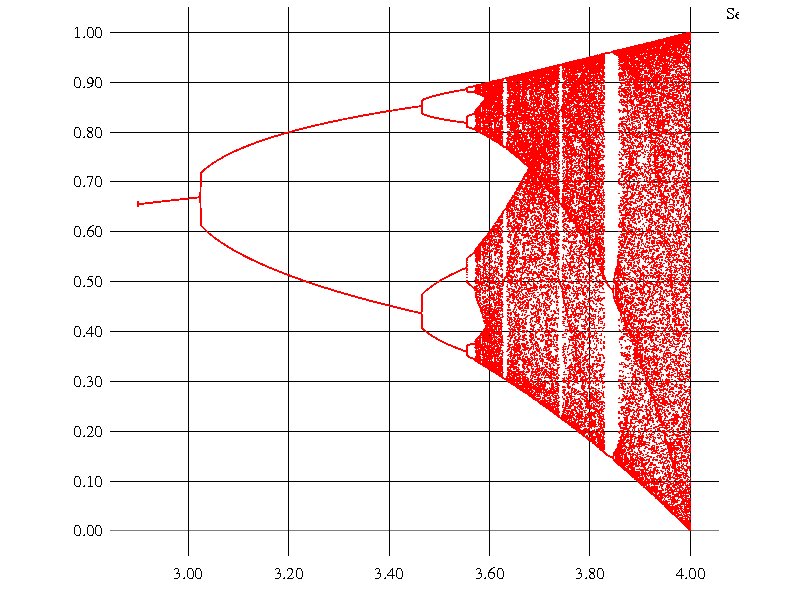
aの値を大きくしている。

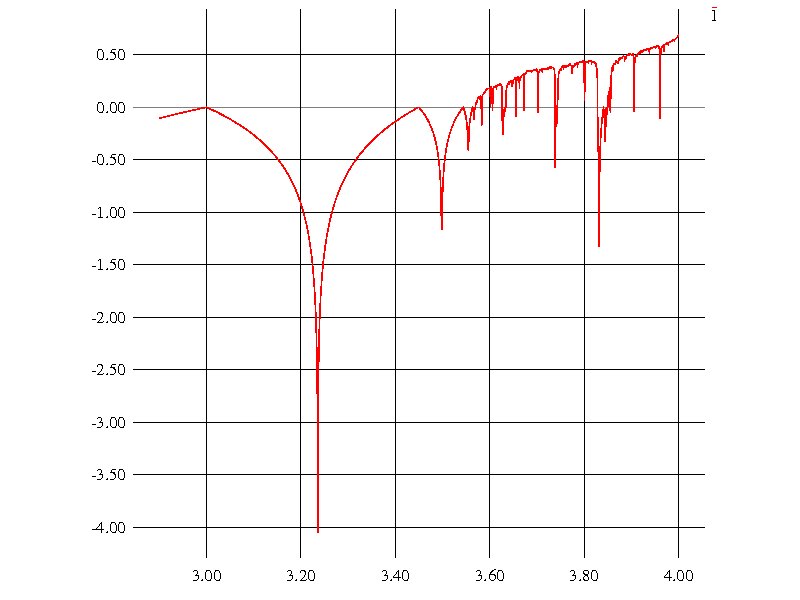
その他カオスを特徴づける方法として、Liapunov Exponentが知られている。その指数が正であるならば、「カオス」であると言われている。

/*
Liapunov Exponent

\lambda=\lim_{n\to \infty}\frac{1}{n}\sum_{j=0}^{n-1}\log |f'(x_j)|

EXAMPLE:
ロジスティック方程式のリアプノフ指数

*/

#include 
#include 

/*初期値設定*/
#define STEP 100000

/*関数宣言*/
double f(double,double);
double g(double,double);

main()
{
  int j;
  double x=0.1,nx,u;
  double liap,h,total;

  for(h=2.9;h<=4.0;h+=0.001)
    {
      for(j=0;j<=STEP-1;j++)
	{
	nx=f(x,h);
	u=fabs(g(nx,h));
	total +=log(u);
	liap = total/STEP;
	x=nx;
	}
       printf("%f %f\n",h, liap);

	nx=0.0;
	u=0.0;
	total=0.0;
	liap=0.0;
    }
 return 0;
}
/*FUNCTION */
double f(double x,double h)
{
  return( h*x*(1.0-x) );
}

/*1st derivative */
double g(double x,double h)
{
  return( h*(1.0-2.0*x) );
}

出力結果

Back to C Language