基本統計量
基本的な統計量を求める関数を紹介する. まず,10人 の患者から成る 2 グループ x,y にそれぞれ異なる睡眠薬を飲ませ,睡眠時間の増加を示すデータを準備する.
x <- c(0.7,-1.6,-0.2,-1.2,-0.1,3.4,3.7,0.8,0.0,2.0) # グループ 1 の睡眠時間の増加を示すデータ y <- c(1.9, 0.8, 1.1, 0.1,-0.1,4.4,5.5,1.6,4.6,3.4) # グループ 2 の睡眠時間の増加を示すデータ |
データを読み込ませた後は,次に紹介する関数で基本統計量を求めることになる.
|
関数 |
ave(x) |
fivenum(x) |
IQR(x) |
max(x) |
mean(x) |
median(x) |
min(x) |
|
意味 |
平均(因子) |
5数要約 |
4分位偏差 |
最大値 |
平均 |
中央値 |
最小値 |
|
|
|||||||
|
関数 |
quantile(x) |
range(x) |
sd(x) |
sum(x) |
var(x,y) |
weighted.mean(x) |
|
|
意味 |
クォンタイル点 |
範囲 |
不偏標準偏差 |
総和 |
不偏分散 |
重み付け平均 |
|
5 数要約:最小値・下側ヒンジ・中央値・上側ヒンジ・最大値
4 分位偏差:第 3 四分位から第 1 四分位を引いた値
クォンタイル点:最小値・第 1 四分位・中央値・第 3 四分位・最大値
範囲:最小値と最大値
また,平方和,歪度及び尖度はそれぞれ
sum((x-mean(x))^2) # 平方和 mean((x-mean(x))^3)/(sd(x)^3) # 歪度 mean((x-mean(x))^4)/(sd(x)^4) # 尖度 |
標本分散と不偏分散,標本標準偏差と不偏標準偏差
データの不偏分散を求める関数 var() は不偏分散を求める関数であって,標本分散を求める関数ではないことに注意.すなわち,データ x のデータ数を n,平均を求める関数を E() とすると,var(x) は以下を求めている.
よって,標本分散を求める場合は var() の結果を (n-1)/n 倍する必要がある.標本標準偏差を求める場合も同様である.
var(x) # 不偏分散 [1] 3.200556 variance <- function(x) var(x)*(length(x)-1)/length(x) # 標本分散を求める関数を定義 variance(x) [1] 2.8805 sd(x) # 不偏標準偏差 [1] 1.789010 sqrt(variance(x)) # 標本標準偏差 [1] 1.697204 |
分散共分散行列・相関行列
2 次元以上のデータに対する不偏共分散(または不偏共分散行列)も関数 var() で求めることが出来る. 引数は 1 次元データを 2 つ与えても,行列を与えても,どちらでも良い. 標本共分散を求める場合は var() の結果を (n-1)/n 倍する必要がある. また,相関係数(または相関行列)は関数 cor() で求めることが出来る.引数は 1 次元データを 2 つ与えても,行列を与えても,どちらでも良い.
var(x, y) [1] 2.848333 cor(x, y) [1] 0.7951702 |
データの規準化
各列が変量となっているデータ行列 x の各変量の単位が異なる場合に,各変量を平均が 0 ,分散が 1 になるように変換することがある.これを規準化または標準化という.関数 scale(x) を用いることで,データ行列 x を標準化することが出来る.標準化は平均を 0 にするためのセンタリング (それぞれの変量からその変量の平均を引く) ,分散を 1 にするためのスケーリング (それぞれの変量をその変量の標準偏差で割る) の 2 つの操作によって行なわれる.なお,センタリングを行なった前後で標準偏差は変わらない.
scale(x)
[,1]
[1,] -0.02794842
[2,] -1.31357592
................
[10,] 0.69871059
attr(,"scaled:center")
[1] 0.75
attr(,"scaled:scale")
[1] 1.789010
|
関数 scale() に center=F と指定することによってセンタリングを抑制することが出来,scale=F と指定することによってスケーリングを抑制することが出来る.
確率分布と乱数
R ではさまざまな理論分布の確率密度 f(x) ,累積分布 P(X ≦ x) ,確率点 min{ x : P(X ≦ x) > q } ,及びその分布に従う乱数を求めることが出来る.
確率分布と乱数に関する関数の使い方
後に紹介する確率分布に関する関数を使用する場合は,以下のような対応表を用いればよい. この表は,確率分布名が xxx である分布の確率点は “qxxx” で求めることが出来ることを表す.例えば t 分布ならば,この累積分布は pt ,確率点は qt で求めることが出来る.
|
用途 |
関数名 |
説明 |
|
確率密度 |
dxxx(q) |
q は確率点を表す.例えばコード名が norm ならば dnorm(q) となる. |
|
累積分布 |
pxxx(q) |
q は確率点を表す.例えばコード名が norm ならば pnorm(q) となる. |
|
確率点 |
qxxx(p) |
p は確率を表す.例えばコード名が norm ならば qnorm(p) となる. |
|
乱数 |
rxxx(n) |
n は生成する乱数の個数を表す.例えばコード名が norm ならば rnorm(n) となる. |
Rに用意されている確率分布
R では以下の理論分布が用意されている.ただし,スチューデント化された分布は qtukey (確率点) と ptukey (累積分布) を求める関数のみ,多項分布は dmultinom(確率密度)と rmultinom(乱数)のみ,誕生日問題の分布(近似解)は pbirthday(一致確率)と qbirthday(一致確率に必要な観測数)のみしか用意されていない.
|
分布名 |
コード名 |
パラメータ |
|
ベータ分布 |
beta |
shape1, shape2, ncp |
|
二項分布 |
binom |
size, prob |
|
コーシー分布 |
cauchy |
location, scale |
|
カイ二乗分布 |
chisq |
df, ncp |
|
指数分布 |
exp |
rate |
|
F分布 |
f |
df1, df2, ncp |
|
ガンマ分布 |
gamma |
shape, scale |
|
幾何分布 |
geom |
prob |
|
超幾何分布 |
hyper |
n, m, k |
|
対数正規分布 |
lnorm |
meanlog, sdlog |
|
ロジスティック分布 |
logis |
location, scale |
|
多項分布 |
multinom |
n, size, prob |
|
負の二項分布 |
nbinom |
size, prob |
|
正規分布 |
norm |
mean, sd |
|
ポアソン分布 |
pois |
lambda |
|
ウィルコクソンの符号付順位和統計量の分布 |
signrank |
m, n |
|
t 分布 |
t |
df, ncp |
|
一様分布 |
unif |
min, max |
|
スチューデント化された分布 |
tukey |
nmeans, df |
|
ワイブル分布 |
weibull |
shape, scale |
|
ウィルコクソンの順位和統計量の分布 |
wilcox |
m, n |
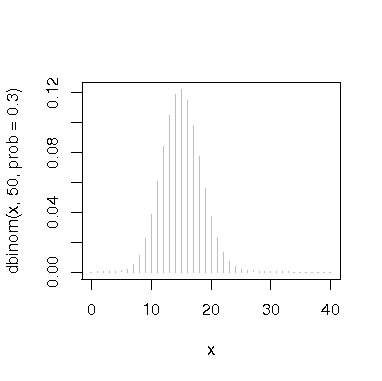
例
plot(x,dbinom(x,50,prob=0.3),type="h",col="gray") # 二項分布(x : ベクトル, prob : 成功の確率) |
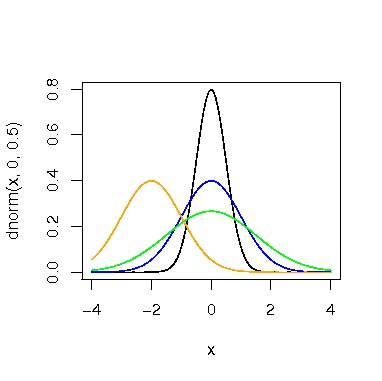
> x<-seq(04,4,0.1) > curve(dnorm(x,0,0.5),from=-4,to=4,type="l") # 正規分布 > curve(dnorm(x,0,1),add=T,col="blue") > curve(dnorm(x,0,1.5),add=T,col="green") > curve(dnorm(x,-2,1),add=T,col="orange") |
正規分布 norm について確率密度 f(x) ,その分布に従う乱数を求めるには以下の様にすればよい.
dnorm(0) # 確率密度 (離散分布の場合は確率関数) [1] 0.3989423 rnorm(5) # 正規分布に従う乱数を 5 個生成 [1] -2.0024918 -0.5996763 -0.3108348 1.2590405 0.3661534 |
確率密度のグラフを描くには以下のようにする.
curve(dnorm, -4, 4, type="l") # 正規分布 plot(0:10, dbinom(0:10, 10, 0.5), type="h", lwd=5) # 二項分布 |
自由度 (p, n - p - 1) の F 分布の上側 100×α 点は qf(1-α, p, n-p-1 ) で求められるので,例えば自由度 (2, 3) の F 分布の上側 5% 点は以下の様にして求めることが出来る.
qf(0.95, 2, 3) # qf(0.05, 2, 3, lower=F) でも可 [1] 9.552094 |
乱数の再現:set.seed() 疑似乱数は R 起動時に初期化され,毎回異なった乱数が発生される . 乱数を再現したい場合は,乱数の種を関数 set.seed() で指定すればよい.
runif(5) # 一様乱数を 5 個生成すると [1] 0.8039566 0.6593698 0.8120159 0.1279622 0.1115031 runif(5) # 当然毎回違った乱数が得られる [1] 0.5694816 0.4504077 0.1823374 0.4573758 0.9061499 set.seed(101); runif(5) # 乱数の種(seed)を指定 [1] 0.37219838 0.04382482 0.70968402 0.65769040 0.24985572 set.seed(101); runif(5) # 乱数の種を同じにすれば乱数を再現することが出来る [1] 0.37219838 0.04382482 0.70968402 0.65769040 0.24985572 |
2 次元正規乱数
相関が r だけある 2 次元正規乱数を生成する関数 r2norm() を定義する.
r2norm <- function(n, mu, sigma, rho) {
tmp <- rnorm(n)
x <- mu+sigma*tmp
y <- rho*x + sqrt(1-rho^2)*rnorm(n)
return(data.frame(x=x,y=y))
}
mydata <- r2norm(100, 0, 1, 0.5)
cor(mydata$x,mydata$y)
[1] 0.5756098
|
Back to R