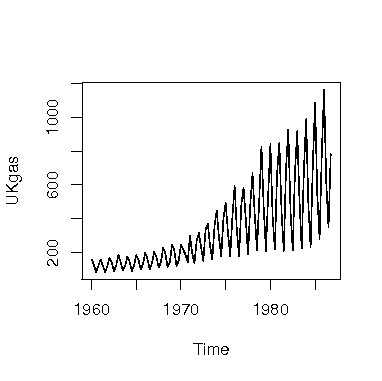
Rには1960年から1986年までのイギリスのガス消費量を四半期ごとに観測した次のような時系列データUKgasがある。
ts.plot(USgas) |
通常のデータの基本的な統計的特性を表す統計量として、平均、分散、相関などが用いられている。これに対応して時系列では、平均、自己共分散(autocovariance)、自己相関(autocorrelation)と呼ばれる統計量がある。
時系列{y1,y2,…,yn-1,yn}の標本平均は
で定義される。時系列の平均や自己共分散の性質が、時間が経過しても変化しない場合、その時系列を定常時系列と言い、それらの性質が何らかの形で変化するものを非定常時系列と言う。
定常時系列について標本データのytとyt-kとの標本自己共分散関数は
標本自己相関関数は
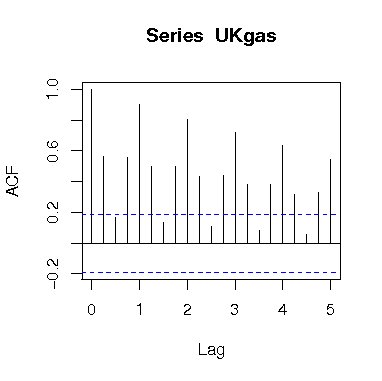
で定義され、次のようにacfという関数で計算することができる.
> acf(x, type =””, plot = TRUE,...), x:data, type:={correlation, covariance or partial}
> acf(UKgas)
|
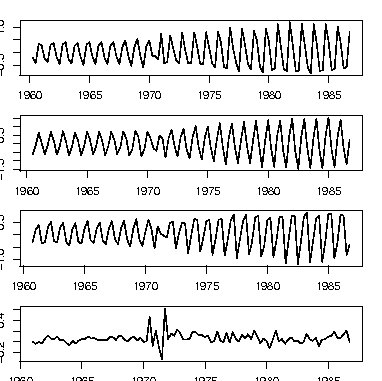
データにおける周期性とトレンドは関数diffを用いて除去することも可能である。 関数diffの引数lagを1、2、3、4にしたデータUKgasの差分を求めるコマンドを次に示す。 ここではまずUKgasを対数変換し、差分を計算している。 これはデータUKgasのトレンドが直線ではなく、指数分布に近似してるからである。
データUKgasは1年を四半期ごとに記録したデータであり、年周期を持っているので、関数diffの引数lagを4にした差分には周期成分が除去される。
また異なる2つの時系列データ間の相互共分散および相互相関は関数ccfで求めることができる。 次にデータmdeathsとfdeathsとの相互相関を求める関数ccfの使用例を示す。 (データmdeathsとfdeathsはデフォルトで入っているもの)
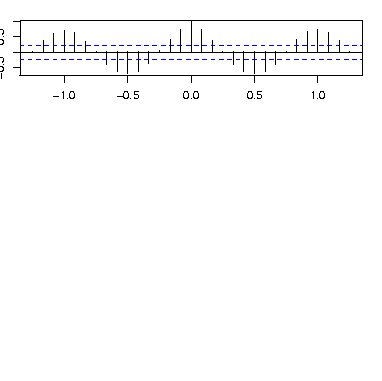
両時系列データは強い相関と周期性を持っていることが読み取れる。 また偏自己共分散・相関は関数pacfで求めることができる。
デコンポジション(要因分解)
> x<-EuStockMarkets[,"DAX"] > x.decomposed<-decompose(x) > plot(x.decomposed) |
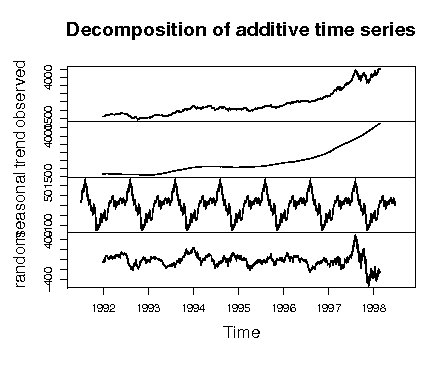
上から順に元々の値・トレンド・季節要因・ノイズと分解される。 また上から季節要因・トレンド・ノイズと順にアクセスできる。 figureってのはseasonalの1単位分の値。つまりseasonalはfigureの繰り返しでできてる。
> str(x.decomposed) List of 5 $ seasonal: Time-Series [1:1820] from 1991 to 1998: 18.3 21.9 26.6 18.2 22.9 ... $ trend : Time-Series [1:1860] from 1991 to 1999: NA NA NA NA NA NA NA NA NA NA ... $ random : Time-Series [1:1820] from 1991 to 1998: NA NA NA NA NA NA NA NA NA NA ... $ figure : num [1:260] 18.3 21.9 26.6 18.2 22.9 ... $ type : chr "additive" - attr(*, "class")= chr "decomposed.ts" |
単位根検定
時系列データのモデルは
Phillips-Perron検定
Rには、Phillips-Perron検定に関する関数PP.testがある。データlhのPP.testの使用例およびその結果を示す。
> PP.test(lh)
Phillips-Perron Unit Root Test
data: lh
Dickey-Fuller = -3.6999, Truncation lag parameter = 3, p-value =
0.03465
|
p値は約0.03であることから単位根があると判断しがたい。
ADF検定
パッケージtseriesにはDickey-Fullerの単位根検定関数adf.testがあり、パッケージfSeries には単位根検定関数adfTest 、unitrootTestなどがある。
データUKgasを用いた関数adf.testの使用例を示す。
> adf.test(UKgas)
Augmented Dickey-Fuller Test
data: UKgas
Dickey-Fuller = -1.6079, Lag order = 4, p-value = 0.7393
alternative hypothesis: stationary
|
p値は約0.7になり、仮説が採択される。 データによっては、非定常データの対数や差分を取ることで定常化することができる。 例えば、データUKgasの1階差分のadf.testを用いた単位根検定のp値は0.01まで下がる。
> adf.test(diff(UKgas))$p.value [1] 0.01 |
共和分検定
スペクトル分析
時系列データは、幾つかの成分が混合されているものと考えられる。例えば、トレンド、周期の成分、ノイズなど。時系列の分析では、周期成分の有無やその成分の値などを分析する必要がある。時系列データに隠されている周期性を解析する方法としてスペクトル解析がある。
時系列における自己共分散Ckのフーリエ変換(Fourier transform)が可能であるとき、周波数
をパワースペクトル密度関数(power spectral density function)、 略してスペクトル(spectrum)と呼ぶ。 また、次式のように上記のパワースペクトル密度関数におけるCkに代わって、 標本データy1,y2,…,ynの標本自己共分散
ただし、周波数は 、 である。 ピリオドグラムはスペクトル密度を推定する1つのツールとして用いられている。
Rには、ピリオドグラムを用いてスペクトル密度関数を推定する関数spec.pgramがある。 関数spec.pgramは、FFT(fast Fourier transform)でピリオドグラム(periodogram)を求め、対数軸(縦軸)のグラフを作成し、引数spansを用いて修正Daniell平滑化を行うことが可能でる。
次に関数spec.pgramによるデータUKgas、ldeathsのピリオドグラムと1組のパラメータによる平滑化のコマンドを示す。
> par(mfrow=c(2,2)) > spec.pgram(UKgas) > spec.pgram(UKgas,spans=c(3,3)) > spec.pgram(ldeaths) > spec.pgram(ldeaths,spans=c(3,3)) |
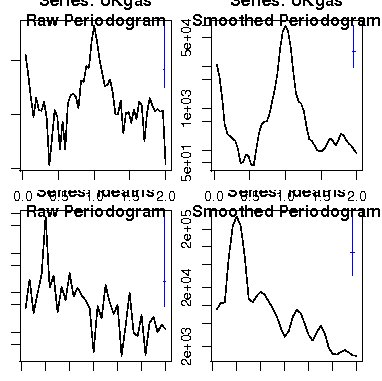
関数spec.pgramによるピリオドグラムのプロットでは、右側の縦のバーは95%信頼区間を示すものである。
Rにはスペクトルを求める関数spectrumがある。この関数spectrumは、関数spec.pgramとspec.arを統合したもので、デフォルトにはspec.pgramが設定されている(method="pgram")。関数spec.arは自己回帰によるスペクトル解析の関数である。次にデータUKgas、ldeathsを用いた自己回帰による関数spectrumの使用例を示す。
> par(mfrow=c(1,2)) > spectrum(UKgas,method="ar") > spectrum(ldeaths,method="ar") |
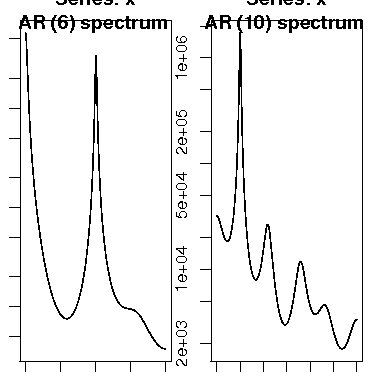
時系列モデル
ARモデル
時系列データの時間t-pからtまでの関係式
を自己回帰モデルと呼ぶ。ai,i=1,2,・・・,pを自己回帰係数と呼び、pを次数(order)と呼ぶ。 次数pであるARモデルを通常AR(p)で表す。 eiは平均0、分散σ2の正規分布に従う残差である。 自己回帰分析は、最も適切な次数pと自己回帰係数。aiを推定することであり、このプロセスをモデルの当てはめ、あるいはモデルの推定と呼ぶ。
ARモデルを当てはめる方法としては、ユールウォーカー(Yule-Walker)法、最小2乗法、最尤法、Burg法など幾つかの方法が提案されている。 モデルの評価にはAIC、BICなどの情報量規準が多く用いられている。
> (lh.ar<-ar(lh))
Call:
ar(x = lh) #ar(x,aic=TRUE,method="",order.max=NULL,...)
Coefficients:
1 2 3
0.6534 -0.0636 -0.2269
Order selected 3 sigma^2 estimated as 0.1959
|
引数xは時系列データオブジェクト、aicはモデルを評価する情報量規準AICを用いるか否かを指定する引数で、デフォルトはTRUEになっているので、AIC情報量規準に基づいてモデルの次数が決められる。 引数methodには、自己回帰モデルを推定する方法、"yule-walker"、"ols"、"mle"、"burg"などの中から1つ選択して指定する。 デフォルトはユールウォーカー(Yule-Walker)法が指定されている。 olsは最小2乗法、mleは最尤法、burgは文字どおりBurg法である。引数order.maxには、次数の最大値を指定することができる。
関数arで作成した自己回帰モデルに関連する項目のリストは、関数summaryを用いて確認することができる。
> summary(lh.ar)
Length Class Mode
order 1 -none- numeric
ar 3 -none- numeric
var.pred 1 -none- numeric
x.mean 1 -none- numeric
aic 17 -none- numeric
n.used 1 -none- numeric
order.max 1 -none- numeric
partialacf 16 -none- numeric
resid 48 ts numeric
method 1 -none- character
series 1 -none- character
frequency 1 -none- numeric
call 2 -none- call
asy.var.coef 9 -none- numeric
|
自己回帰モデルの次数は$oder、係数は$ar、aicの値は$aic、残差は$residで返すことができる。
> lh.ar$order [1] > lh.ar$ar [1] 0.65340168 -0.06362084 -0.22694020 |
上記の値を小数点以下3第位までに丸めた、データlhのAR(3)モデルを次に示す。
◇ モデルの診断
作成したモデルの適切さを判断するためには、残差分析が必要である。ARモデルにおける残差は平均0の正規分布に従い、残差の間には相関がないことを期待する。 Rには、時系列データの独立性を検定する関数Box.testがある。 関数Box.testは、Box-Pierce検定とLjung-Box検定を行う。この関数を用いて残差の独立性を検定することが可能である。
次にAR(3)モデルの残差のLjung-Box検定の例を示す。結果から分かるように、残差が独立である仮説が採択される。
> Box.test(lh.ar$res,type="Ljung")
Box-Ljung test
data: lh.ar$res
X-squared = 0.0257, df = 1, p-value = 0.8728
|
残差の正規性に関しては、パッケージtseriesに時系列データの正規性を検定する関数jarque.bera.testがある。関数jarque.bera.testは欠損値を含んでいるとエラーメッセージを返す。関数arが返す残差の中の先頭のp個(モデルの次数)は欠損値であるので、次のように切り取って用いる。 また、残差の正規性に関してはqqnormを用いて考察を行うことも1つの方法である。
> jarque.bera.test(temp)
Jarque Bera Test
data: temp
X-squared = 7.913, df = 2, p-value = 0.01913
|
◇ 予測
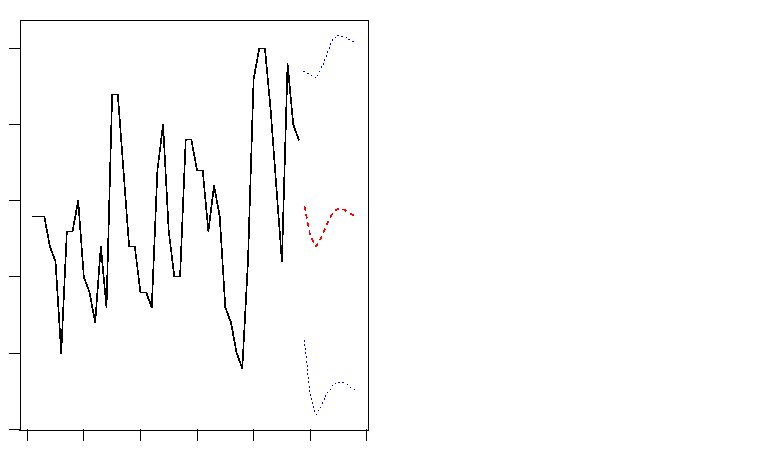
モデルを求める目的の1つは予測である。 自己回帰モデル関数arで求めたモデルによる予測値は関数predictを用いて求めることができる。 作成したモデルを用いた、関数predictの使用例を次に示す。 引数n.aheadには予測の期間を指定する。 関数predictは、予測値$pred、標準残差$seを時系列オブジェクトとして返す。
> (lh.pr<-predict(lh.ar,n.ahead=10)) $pred Time Series: Start = 49 End = 58 Frequency = 1 [1] 2.461588 2.272267 2.199151 2.262914 2.352194 2.423066 2.449223 2.441544 [9] 2.418779 2.398456 $se Time Series: Start = 49 End = 58 Frequency = 1 [1] 0.4425687 0.5286675 0.5525786 0.5527502 0.5592254 0.5665903 0.5688786 [8] 0.5689385 0.5692396 0.5697534 |
次にデータlhを用いた関数predict による10期の自己回帰予測値および2倍の標準残差のプロットを作成する例を示す。
> jarque.bera.test(temp)
Jarque Bera Test
data: temp
X-squared = 7.913, df = 2, p-value = 0.01913
|
ARMAとARIMAモデル
自己回帰モデル
を自己回帰移動平均(ARMA; AutoRegressive Moving Average model)モデルと呼び、 通常ARMA(p,q)で表す。 定義式から分かるようにARモデルはARMAモデルの特殊なケースである。
yiのd階の差分演算子
Rには、単変量時系列データを当てはめるARIMAモデル関数arimaがある。次に関数arimaの書き式を示す。
> (lh.ari<-arima(lh,order = c(2,0,1))) #arima(x,order=c(0,0,0),...)
Call:
arima(x = lh, order = c(2, 0, 1))
Coefficients:
ar1 ar2 ma1 intercept
1.1765 -0.5044 -0.5080 2.3946
s.e. 0.3990 0.2190 0.4517 0.0944
sigma^2 estimated as 0.1827: log likelihood = -27.6, aic = 65.2
|
引数xは、時系列データオブジェクトであり、orderは自己回帰の次数 、差分の階数 、過去の残差の移動平均の次数 を指定する引数である。
返された係数を用いたARIMA(2,0,1)モデルを次に示す。
関数arima結果の項目は、関数summaryで確認できる。
> summary(lh.ari)
Length Class Mode
coef 4 -none- numeric
sigma2 1 -none- numeric
var.coef 16 -none- numeric
mask 4 -none- logical
loglik 1 -none- numeric
aic 1 -none- numeric
arma 7 -none- numeric
residuals 48 ts numeric
call 3 -none- call
series 1 -none- character
code 1 -none- numeric
n.cond 1 -none- numeric
model 10 -none- list
|
モデル評価に関連する情報として、sigma2(残差の分散σ2)、対数尤度$loglik、AIC情報量規準$aic、 残差$residualsなどがある。
関数arimaを用いる際、最も基本的な問題は、引数order のp、d、qを幾らにするかである。 p、d、qを求める1つの方法は、ある範囲内のp、d、qのすべての組み合わせの中から、情報量規準(AICやBICなど)値が最も小さい組み合わせを用いる方法である。
次にデータlhを用いてp、d、qを求める例として、pは1から4まで、dは0から1まで、qは0から4までのすべての組み合わせで最適なp、d、qを求める簡単なプログラムを示す。情報量規準はAICを用いる。
> data<-lh;T<-0
> for(p in 1:4)
+ for(d in 0:1)
+ for(q in 0:4){
+ fit<-arima(data,order=c(p,d,q))
+ T<-T+1
+ if(T==1){
+ minaic<-fit$aic;
+ orderP<-p;orderD<-d;orderQ<-q;
+ }else{
+ if(fit$aic<-minaic){
+ minaic<-fit$aic;
+ orderP<-p;orderD<-d;orderQ<-q;
+ }
+ }
+ }
> cat("Result:p=",orderP,"d=",orderD,"q=",orderQ,"AIC=",minaic,"\n");
Result:p= 4 d= 1 q= 4 AIC= 64.75832
|
求めたp、d、qはそれぞれ、3、0、0である。 (もちろんこの結果は、AR(3)モデルと同じである。)
> (lh.ari<-arima(lh,order=c(3,0,0)))
Call:
arima(x = lh, order = c(3, 0, 0))
Coefficients:
ar1 ar2 ar3 intercept
0.6448 -0.0634 -0.2198 2.3931
s.e. 0.1394 0.1668 0.1421 0.0963
sigma^2 estimated as 0.1787: log likelihood = -27.09, aic = 64.18
|
返される結果を用いたARIMA(3,0,0)モデルを次に示す。
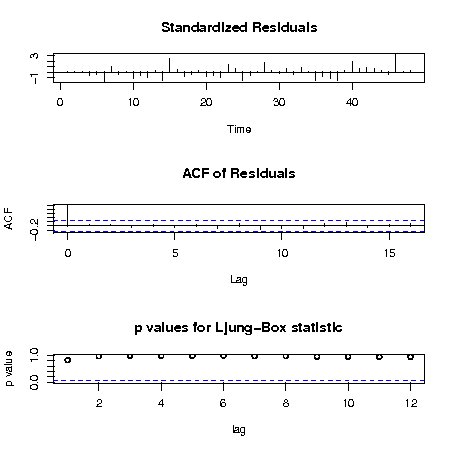
ARIMAモデルを診断(残差分析)するツールとして関数tsdiagがある。 データlhのARIMA(3,0,0)モデルの診断図を次に示す。 診断図の上部は、残差のプロット、中部は残差の自己相関のプロット、下部は引数gof.lagに対応するLjung-Box検定のp値のプロットである。 これから、残差の平均がゼロであり、分散が一定、残差が自己相関が存在しない事を確認すれば良い。 Ljung-Box検定は、帰無仮説が、残差に自己相関は存在しない、というもので、 p値はその帰無仮説を棄却した時に誤る確率を表している。 よってp値が大きいほど、帰無仮説は棄却されず、推定結果が有意という事になる。
> tsdiag(fit,gof.lag=12) |
関数arimaで求めたモデルの予測値は、関数predictを用いて求めることができる。
ARFIMAモデル
ARIMAモデルは、過剰の差分が起こり得ることがあると指摘されている。 その短所を克服するため、差分の階数dが整数に限らず、任意の実数に一般化した方法が自己回帰実数和分移動平均(ARFIMA; AutoRegressive Fractionally Integrated Moving Average)モデルである。 ARFIMA モデルは差分要素を2項級数展開することで実数dを取ることを可能にしている。 fracdiff(x, nar = 0,dtol = NULL,nma = 0,…): 引数xは時系列データで、引数narは自己回帰の次数p、引数dtolは差分の階数d、引数nmaは移動平均の次数qを指定する引数である。 ここではデータAirPassengersを用いて、まず差分階数を推定し、その結果を用いてARFIMA(3,d,1)モデルの係数を推定する例を示す。データAirPassengersは、ある航空会社の1949年から1960年までの国際旅客数に関する時系列データである。
> library(fracdiff)
> (AP.d<-fdGPH(AirPassengers)$d)
[1] 0.6513916
> AP.fra<-fracdiff(AirPassengers,nar=3,dtol=AP.d,nma=1)
> summary(AP.fra)
Call:
fracdiff(x = AirPassengers, nar = 3, nma = 1, dtol = AP.d)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
d 4.604e-01 1.442e-01 3.192 0.00141 **
ar1 -1.159e-02 5.996e-05 -193.222 < 2e-16 ***
ar2 3.295e-01 3.103e-01 1.062 0.28826
ar3 -1.266e-01 7.667e-05 -1650.804 < 2e-16 ***
ma -9.009e-01 1.197e-01 -7.527 5.2e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
[d.tol = 0.1, M = 100, h = 7.322e-06]
Log likelihood: -693.9 ==> AIC = 1389.788 [1 deg.freedom]
|
最大対数尤度は$log.likelihood、自己回帰係数は$ar、移動平均係数は$maで返すことができる。
非定常時系列モデル(ARCH, GARCH)
時系列データが、条件付き平均gt、条件付き分散htの正規分布N(gt,ht)に従うとき、htの変動を
さらに、ARCHモデルを次のように拡張したものをGARCH(Generalized ARCH)モデルと呼ぶ。
また、条件付き分散の非対称性を表すTGARCH(Threshold GARCH)モデル、GARCHモデルとTGARCHモデルを統合したAPARCH(Asymmetric Power ARCH)モデルも提案されている.
準備中。
成分の分解(ARCH, GARCH)
時系列データには周期的に変動する周期性質を持つものも少なくない。 一定の期間で周期的に変動する時系列データについて、それを幾つかの成分に分解することによって、より詳細に分析を行うことができる。
典型的な例として次のモデルがある。
観測値=トレンド+周期変動+残差
ここの場合のトレンドは、比較的に滑らかな長期変動を示すものであり、周期変動は、週・月・四半期など時間あるいは時節とともに一定のリズムで周期的に変動する成分で、季節変動(あるいは季節成分)とも呼ばれている。
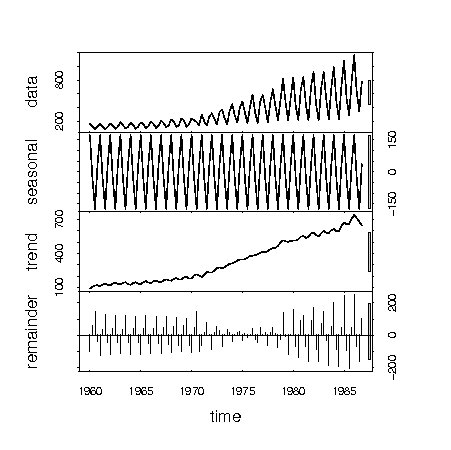
Rには時系列データを、トレンド、周期変動、残差に分解する関数stlがある。関数stlを用いてデータUKgasをトレンド、季節変動、残差に分解したプロットを次のように示す。 関数stlでは、引数s.windowに季節成分を抽出する条件として、文字列"periodic"(略してperでもよい)を指定するか、あるいはラグの値を指定する必要がある。
> plot(stl(UKgas, s.window ="per")) |
Back to R