常微分方程式
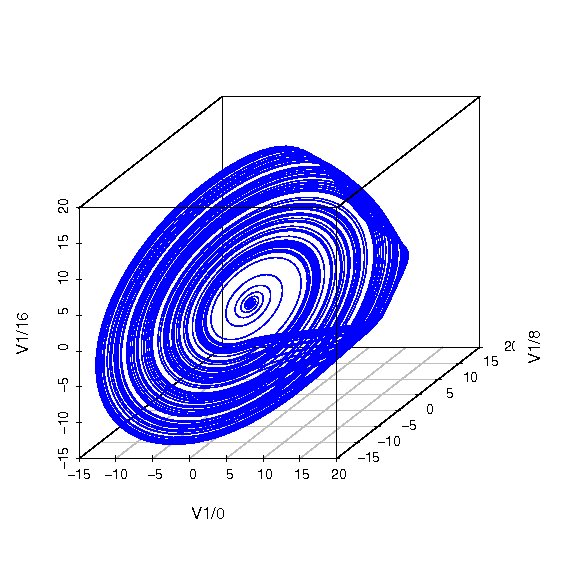
非線形微分方程式
> library(tseriesChaos) > library(scatterplot3d) > ro.em<-embedd(rossler.ts,m=3,d=8) > scatterplot3d(ro.em,type="l",color=4) |
偏微分方程式
確率微分方程式
確率微分方程式:
においてEulerの離散化を考える:
となり、初期値をt0=0,y0=X0=100,W0=0 として、 刻み幅Δtでj=0,1,2,...で次のループを回すことになる。
tj+1=tj+Δt,
ΔW=Z with Z〜N(0,1)
yj+1=yj+a(yj,tj)Δt+b(yj,tj)ΔW
> simu.sde01<-function(x0=100,aa=0.1,bb=0.2,nn=5,mm=300,dt=1/300){
+ for(i in 1:nn){
+ xx<-rnorm(mm)
+ yy<-x0
+ for(j in 1:mm){
+ yy.t<-yy[j]
+ yy<-c(yy,yy.t+aa*yy.t*dt+bb*yy.t*xx[j]*sqrt(dt))
+ }
+ plot(yy,type="l",ylim=c(max(0,x0-abs(aa)*mm),x0+abs(aa)*mm))
+ par(new=T)
+ }
+ title("Simulation of SDE")
+ }
|
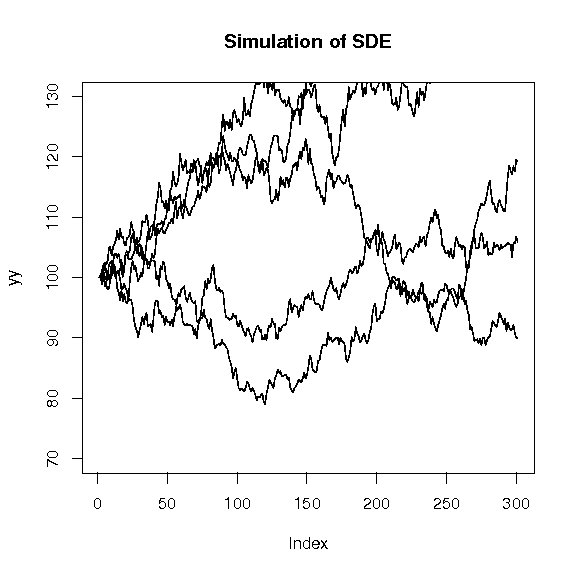
のシミュレーションを5回行い、これを
> simu.sde01(100,0.1,0.2,5,300,1/300) |
Back to R