R-Principal Component Analysis

１．基本概念
　実験などでは通常個体の属性を複数の項目（変数）に分けて記録する。変数が少ない場合は簡単なグラフや基本統計量などでデータの構造を明らかにすることができるが、変数が多くなるとデータの構造が複雑になり、解析が難しくなる。一方、変数が多くなると変数の間には相関がある可能性も増える。そこで主成分分析(principal component analysis)とは多くの変数により記述された量的データの変数間の相関を排除し、できるだけ少ない情報の損失で、少数個の無相関な合成変数に縮約して、分析を行う手法である。
　例）　表1の左側に示す3つの個体の2次元データ(x1, x2)があるとする。そのx1を横軸、x2を縦軸にした座標系上の散布図を図１(a)に示す。図１(a)の個体は、座標軸x1の値x1iと座標軸x2の値x2i（i=1,2,3 )、つまり2次元で表記しなければならない。しかし、この座標系を図1(b)のようなz1 , z2 の座標系に変換すると1変数のみで表すことができる。

表1　二次元のデータの例
	x1	x2	変換	z1	z2
個体1	1	2	⇒	2.236	0.000
個体2	2	4	⇒	4.472	0.000
個体3	3	6	⇒	6.708	0.000
分散	1	4	⇒	5.000	0.000
相関係数	1		⇒	0

図1　座標の変換
(a)	変換 ⇒	(b)

このように図１(b)の中の新しい座標 z1 から x1, x2 へ一種の座標変換を行うことができる。よって主成分分析とは合成変数(線形結合式)の係数を主成分と呼び、主成分分析での主な問題は、いかにデータを縮約する係数(主成分)を求めるかのことを言う。

　次にこれを一般化する。 m 個の個体、 n個の変数(x1,x2, ･･･,xn)により構成された表2のようなデータセットがあり、これをXm×nで表す。

表2　データ(Xm×n)

　このn次元のデータをより低い k(k≦n)次元に縮約する線形結合の一般式を次に示す。

この線形結合式z1に用いる係数を第1主成分、z2に用いた係数を第2主成分と呼び、次のようにAm×kを定義する。

表3　係数データ(Am×k)

データXm×nと係数Am×kを線形結合式で求めた値zjを主成分得点と呼ぶ。主成分得点のデータ(Zm×k)を表4に示す。主成分得点Zm×kとデータ、係数Am×kとの関係は、Zm×k=Xm×n An×k(行列の演算)となる。

表4　主成分得点(Zm×k)

分散(相関)を最大にする方法で主成分を求めることは、データの分散共分散行列(相関係数行列)の固有値と固有ベクトルを求める問題に帰する。その固有ベクトルが主成分であり、固有値の大小がそれに対応する固有ベクトル(主成分)に含まれる情報の多少を決める。
　データの分散共分散行列(あるいは相関係数行列)の固有値λiは通常で表記する。固有値を求めるアルゴリズムは、固有値を大小の降順に並べて返す。

固有値は主成分得点の標準偏差の2乗に等しい。この値が大きい主成分(固有ベクトル)ほど、元のデータの情報を多く含んでいる。最も大きい固有値に対応する主成分を第１主成分、その次に大きい固有値に対応する主成分を第２主成分と呼ぶ。ある主成分にデータ全体の情報がどれぐらい含まれているかは、その主成分に対応する固有値(標準偏差)が固有値全体(標準偏差全体)の中でどれぐらいの割合を占めているかで説明できる各固有値が固有値全体に占める割合を寄与率、その寄与率を累積したものを累積寄与率と呼ぶ。主成分分析を行う際には、寄与率が大きい少数個の主成分を用いる。つまりq個の主成分にデータ全体の何割の情報が含まれているかは、第主成分までの累積寄与率を用いて説明する。

２．使用例
主成分分析を行なう場合は関数 prcomp() を用いる。

 
> prcomp(USArrests)
Standard deviations:
[1] 83.732400 14.212402  6.489426  2.482790

Rotation:
                PC1         PC2         PC3         PC4
Murder   0.04170432 -0.04482166  0.07989066 -0.99492173
Assault  0.99522128 -0.05876003 -0.06756974  0.03893830
UrbanPop 0.04633575  0.97685748 -0.20054629 -0.05816914
Rape     0.07515550  0.20071807  0.97408059  0.07232502

> prcomp(USArrests,scale=TRUE)
Standard deviations:
[1] 1.5748783 0.9948694 0.5971291 0.4164494

Rotation:
                PC1        PC2        PC3         PC4
Murder   -0.5358995  0.4181809 -0.3412327  0.64922780
Assault  -0.5831836  0.1879856 -0.2681484 -0.74340748
UrbanPop -0.2781909 -0.8728062 -0.3780158  0.13387773
Rape     -0.5434321 -0.1673186  0.8177779  0.08902432

> plot(prcomp(USArrests))
> 
> summary(prcomp(USArrests,scale=TRUE))

Importance of components:
                          PC1    PC2     PC3     PC4
Standard deviation     1.5749 0.9949 0.59713 0.41645
Proportion of Variance 0.6201 0.2474 0.08914 0.04336
Cumulative Proportion  0.6201 0.8675 0.95664 1.00000

３．関数
　20ケース、5変数の架空データrnorm関数とmatrix関数を使用して、その主成分分析を説明する。

 
> set.seed(123)
> x<-matrix(rnorm(100),ncol=5)
> colnames(x)<-paste("X",1:5,sep="")
> ans<-prcomp(x,scale=TRUE)
> print(ans)
Standard deviations:
[1] 1.2319356 1.1243639 1.0686284 0.8771723 0.5538435

Rotation:
           PC1         PC2         PC3        PC4        PC5
X1  0.30679471 -0.58628528  0.07987106  0.7274516  0.1630380
X2 -0.53412942 -0.03931111 -0.58309420  0.3670419 -0.4883050
X3  0.32744133  0.50401972 -0.59599796  0.2254383  0.4824006
X4 -0.08614867 -0.62731465 -0.48237333 -0.4945129  0.3490382
X5 -0.71129695  0.08464427  0.25636726  0.2018143  0.6167972

主成分負荷量について
prcompが表示する固有ベクトルは、主成分得点を計算する際の重みを示しているが、しかし多くの教科書では因子分析との関連から主成分負荷量を示している。主成分負荷量を計算するには固有値と固有ベクトルが必要である。
　prcomp関数が返すオブジェクトの構造はstr関数を使用すれば分かる。変数ansに付値されているオブジェクトの構造は以下のようになっている。

 
> str(ans)
List of 5
 $ sdev    : num [1:5] 1.232 1.124 1.069 0.877 0.554
 $ rotation: num [1:5, 1:5] 0.3068 -0.5341 0.3274 -0.0861 -0.7113 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:5] "X1" "X2" "X3" "X4" ...
  .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
 $ center  : Named num [1:5] 0.1416 -0.0513 0.1065 -0.1199 0.3751
  ..- attr(*, "names")= chr [1:5] "X1" "X2" "X3" "X4" ...
 $ scale   : Named num [1:5] 0.973 0.83 0.957 0.973 0.829
  ..- attr(*, "names")= chr [1:5] "X1" "X2" "X3" "X4" ...
 $ x       : num [1:20, 1:5] 0.4314 -0.0924 1.2638 0.9676 1.3374 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
 - attr(*, "class")= chr "prcomp"

　固有値の平方根は要素名 sdev, 固有ベクトルは要素名 rotationに付値されている。これらを使うことにより、主成分負荷量と固有値は以下のようにして求めることができる。

 
> t(t(ans$rotation)*ans$sdev) # 主成分負荷量
          PC1         PC2         PC3        PC4         PC5
X1  0.3779513 -0.65919800  0.08535248  0.6381004  0.09029754
X2 -0.6580131 -0.04419999 -0.62311100  0.3219590 -0.27044455
X3  0.4033866  0.56670158 -0.63690032  0.1977482  0.26717440
X4 -0.1061296 -0.70532995 -0.51547782 -0.4337731  0.19331252
X5 -0.8762721  0.09517096  0.27396132  0.1770259  0.34160912

> ans$sdev^2  # 固有値
[1] 1.5176654 1.2641942 1.1419666 0.7694313 0.3067426

以上のような計算をまとめて行うために、以下のようなprcomp3関数を定義しておく。主成分負荷量はloadings, 固有値はeigenvaluesという名前要素にそれぞれ付値し、 prcompが返すほかの結果とともに表示するようにし、それらがオブジェクトとして非表示で返されるようになっている。

 
> prcomp3<-function(df)
+ {
+ df<-na.omit(df)
+ ans<-prcomp(df,scale=TRUE)
+ ans$loadings<-t(t(ans$rotation)*ans$sdev)
+ ans$eigenvalues<-ans$sdev^2
+ print.default(ans)
+ invisible(ans)
+ }

使用例

 
> set.seed(123)
> x<-matrix(rnorm(100),ncol=5)
> colnames(x)<-paste("X",1:5,sep="")
> ans3<-prcomp3(x)
$sdev
[1] 1.2319356 1.1243639 1.0686284 0.8771723 0.5538435

$rotation
           PC1         PC2         PC3        PC4        PC5
X1  0.30679471 -0.58628528  0.07987106  0.7274516  0.1630380
X2 -0.53412942 -0.03931111 -0.58309420  0.3670419 -0.4883050
X3  0.32744133  0.50401972 -0.59599796  0.2254383  0.4824006
X4 -0.08614867 -0.62731465 -0.48237333 -0.4945129  0.3490382
X5 -0.71129695  0.08464427  0.25636726  0.2018143  0.6167972

$center
         X1          X2          X3          X4          X5 
 0.14162380 -0.05125716  0.10648523 -0.11991706  0.37509474 

$scale
       X1        X2        X3        X4        X5 
0.9726653 0.8299387 0.9573406 0.9731062 0.8289955 

$x
              PC1        PC2          PC3         PC4         PC5
 [1,]  0.43141998 -0.3102117  0.793499624 -1.50711896 -0.01890350
 [2,] -0.09239762  0.3140370  0.475044710 -0.22902545 -0.25224192
 [3,]  1.26382609 -1.4689078  1.530374849  0.23253077 -0.51161747
 [4,]  0.96761811  1.7676268 -0.285009417  0.65504205  1.30406490
 [5,]  1.33741382  1.1673338  0.004045901  0.33513012  0.10600181
 [6,]  1.12793355 -1.7956982  1.820413098 -0.06178608  0.72603917
 [7,] -1.31524829 -0.7952911 -0.339713432  0.39902414  0.01454694
 [8,] -0.83828404  0.4311177  0.030396966 -1.16976738 -0.53825819
 [9,]  1.17775979  0.1620042 -0.457103668 -1.64197252  0.69220578
[10,] -1.94606282 -1.1276733 -1.683350545 -0.82116033  0.39204803
[11,] -0.41355815 -0.2954055  0.037046057  1.39455591  0.30135858
[12,]  0.22466500  1.2379406  1.412095867  1.17828110 -0.54432678
[13,] -0.56106645 -1.0192427 -1.150805724 -0.02804836 -0.28634077
[14,]  0.73655750  0.9165783 -1.459313572  0.74037945 -0.87365820
[15,] -1.69071092  0.6709873  0.122730748  0.31476385 -0.26835874
[16,]  1.26049754 -1.1224650 -2.131976886  1.07019496  0.23611823
[17,] -2.38360857 -0.8235202  1.276704629  0.66923356  0.15880744
[18,] -1.39030318  2.3508168  0.440338726 -0.62766802  0.36019897
[19,]  0.84382127 -0.5727235 -0.124105804  0.00829820 -0.09397289
[20,]  1.25972740  0.3126966 -0.311312129 -0.91088703 -0.90371139

$loadings
          PC1         PC2         PC3        PC4         PC5
X1  0.3779513 -0.65919800  0.08535248  0.6381004  0.09029754
X2 -0.6580131 -0.04419999 -0.62311100  0.3219590 -0.27044455
X3  0.4033866  0.56670158 -0.63690032  0.1977482  0.26717440
X4 -0.1061296 -0.70532995 -0.51547782 -0.4337731  0.19331252
X5 -0.8762721  0.09517096  0.27396132  0.1770259  0.34160912

$eigenvalues
[1] 1.5176654 1.2641942 1.1419666 0.7694313 0.3067426

attr(,"class")
[1] "prcomp"

主成分が持つ情報量
　主成分分析は元のデータが持つ情報を少数個の主成分で要約する手法である。元のデータにp個の変数があれば、主成分は第1主成分から第p主成分まである。それぞれの主成分が元の情報をどれくらいようやくしているかを表すのは、主成分に対応する固有値の大きさである。今の場合第1主成分に対する固有値は1.518である。

 
> ans3$eigenvalues
[1] 1.5176654 1.2641942 1.1419666 0.7694313 0.3067426

5つの主成分の固有値の和はp=5である。つまり元のp個の変数は、それぞれが大きさ1の情報量を持つ。 p個の変数は全体で大きさpの情報を持つ。主成分が持つ情報の全体の情報に対する割合は、固有値をpで割ったものに等しい。今の場合、第1主成分が持つ情報の割合は1.518/5=0.304になる。

 
> sum(ans3$eigenvalues) # 固有値の合計
[1] 5
> cumsum(ans3$eigenvalues)　# 固有値の累積和
[1] 1.517665 2.781860 3.923826 4.693257 5.000000

主成分のうちで意味があるのは、対応する固有値が1以上のものである。固有値が1未満ということは、その主成分が持っている情報が元の変数の1つ分に満たない、つまり1人前の主成分ではないことを意味する。今の場合では固有値が1以上のものは3つであるから、第3主成分までを採用することになる。第3主成分の主成分で元の情報のほぼ80％を要約したことを意味する。

 
> (ans4<-ans3$eigenvalues/sum(ans3$eigenvalues)) #寄与率
[1] 0.30353309 0.25283883 0.22839331 0.15388625 0.06134852

> cumsum(ans4) #累積寄与率
[1] 0.3035331 0.5563719 0.7847652 0.9386515 1.0000000

> screeplot(prcomp(x))

主成分得点について

 
> ans3$x
              PC1        PC2          PC3         PC4         PC5
 [1,]  0.43141998 -0.3102117  0.793499624 -1.50711896 -0.01890350
 [2,] -0.09239762  0.3140370  0.475044710 -0.22902545 -0.25224192
 [3,]  1.26382609 -1.4689078  1.530374849  0.23253077 -0.51161747
 [4,]  0.96761811  1.7676268 -0.285009417  0.65504205  1.30406490
 [5,]  1.33741382  1.1673338  0.004045901  0.33513012  0.10600181
 [6,]  1.12793355 -1.7956982  1.820413098 -0.06178608  0.72603917
 [7,] -1.31524829 -0.7952911 -0.339713432  0.39902414  0.01454694
 [8,] -0.83828404  0.4311177  0.030396966 -1.16976738 -0.53825819
 [9,]  1.17775979  0.1620042 -0.457103668 -1.64197252  0.69220578
[10,] -1.94606282 -1.1276733 -1.683350545 -0.82116033  0.39204803
[11,] -0.41355815 -0.2954055  0.037046057  1.39455591  0.30135858
[12,]  0.22466500  1.2379406  1.412095867  1.17828110 -0.54432678
[13,] -0.56106645 -1.0192427 -1.150805724 -0.02804836 -0.28634077
[14,]  0.73655750  0.9165783 -1.459313572  0.74037945 -0.87365820
[15,] -1.69071092  0.6709873  0.122730748  0.31476385 -0.26835874
[16,]  1.26049754 -1.1224650 -2.131976886  1.07019496  0.23611823
[17,] -2.38360857 -0.8235202  1.276704629  0.66923356  0.15880744
[18,] -1.39030318  2.3508168  0.440338726 -0.62766802  0.36019897
[19,]  0.84382127 -0.5727235 -0.124105804  0.00829820 -0.09397289
[20,]  1.25972740  0.3126966 -0.311312129 -0.91088703 -0.90371139

この主成分得点は、各主成分ごとの平均値は0、不偏分散は固有値に対応している。また各主成分得点の相関は0で、直交している。

 
> colMeans(ans3$x) # 主成分得点の平均値
          PC1           PC2           PC3           PC4           PC5 
 4.579670e-17 -6.938894e-18 -1.040834e-18 -1.214306e-17  1.665335e-17 

> apply(ans3$x,2,var) # 主成分得点の不偏分散
      PC1       PC2       PC3       PC4       PC5 
1.5176654 1.2641942 1.1419666 0.7694313 0.3067426 

> cor(ans3$x)　# 主成分得点間の相関は0
              PC1           PC2           PC3           PC4           PC5
PC1  1.000000e+00  4.687405e-16 -2.660361e-16 -2.217168e-16 -3.732909e-16
PC2  4.687405e-16  1.000000e+00  3.110567e-17  2.534608e-16 -1.170160e-16
PC3 -2.660361e-16  3.110567e-17  1.000000e+00 -3.169654e-16  8.222963e-16
PC4 -2.217168e-16  2.534608e-16 -3.169654e-16  1.000000e+00 -2.582914e-17
PC5 -3.732909e-16 -1.170160e-16  8.222963e-16 -2.582914e-17  1.000000e+00

主成分の意味付け
主成分負荷量は、主成分と元の変数との相関係数に相当するものである

 
> ans3$loadings
          PC1         PC2         PC3        PC4         PC5
X1  0.3779513 -0.65919800  0.08535248  0.6381004  0.09029754
X2 -0.6580131 -0.04419999 -0.62311100  0.3219590 -0.27044455
X3  0.4033866  0.56670158 -0.63690032  0.1977482  0.26717440
X4 -0.1061296 -0.70532995 -0.51547782 -0.4337731  0.19331252
X5 -0.8762721  0.09517096  0.27396132  0.1770259  0.34160912

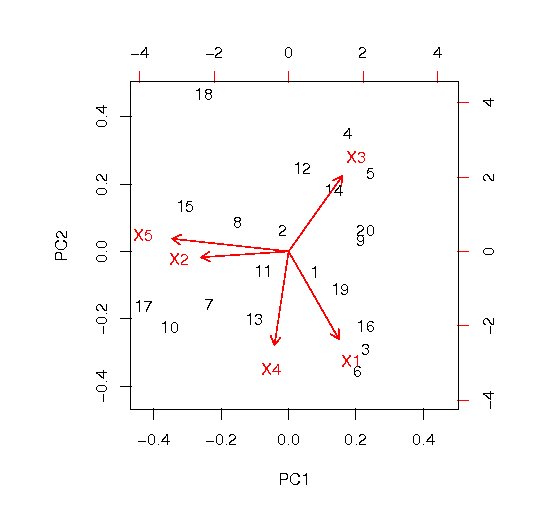
例えば上の分析例の第3主成分PC3は、X3との相関は-0.637, X5との相関は0.274なので、X3とX5は正反対の関係にあると分かる。
変数と主成分の関係を解釈するために、2つずつの主成分の組み合わせて図を作成する。原点付近に位置する変数は、それぞれの主成分とあまり相関のないものである。両端に離れるほど相関が強くなる。原点を中心として両極端にある変数は互いに逆の性質を持っていることが一目で分かる。

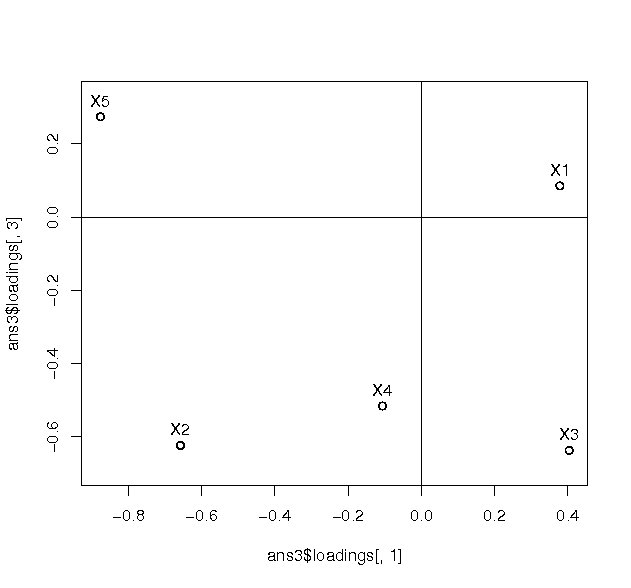
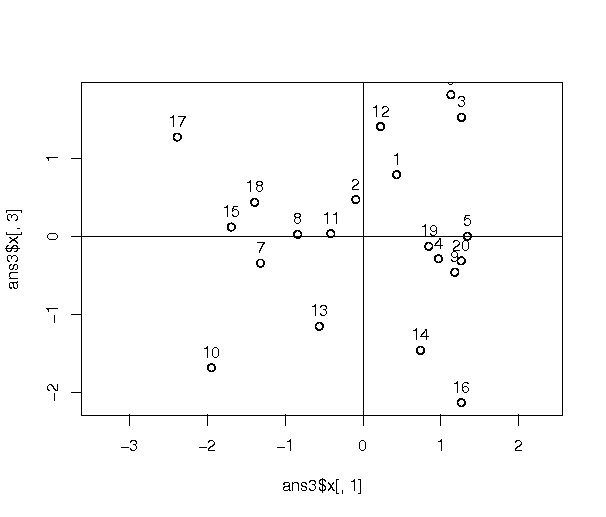
主成分の得点に関しても同様の図を作成する。それぞれの主成分負荷量が正あるいは負の値をとったときの意味は、主成分得点に反映される。次の図において、第1主成分得点(横軸)が負の値をとる17番や10番のケースはX2やX5と関係が深いが、第3主成分の観点から見ると両社は逆の関係にあるといったことが読み取れる。

主成分負荷量と主成分得点を1つの図に表現する。 biplotというものがある。

biplot(procompが返すオブジェクト, choices=c(数値1, 数値2)

choices引数は描画する2つの主成分を指定するためのものであり、 2つの要素を持つ整数ベクトルである。数値1で指定された主成分が横軸、数値2で指定された主成分が縦軸にスケールを調整して描画される。

矢印で表されるのが主成分負荷量である。矢印の先が主成分負荷量の値であり、変数名が描かれる。各ケースの主成分得点は番号の位置で表される。

なおテキストデータにおいても主成分分析を使用できる。
テキストデータの分析

Back to R