ランダム行列
ランダム行列というのは行列の成分がある分布に従っている場合の行列のことを言います。 ここではこのランダム行列の固有値の分布を調べてみると、 特徴的な形をしていることが知られています。
例えば、固有値の分布がWignerの半円則に従うものやGirkoの円則などが有名です。
またこの理論は物理学で生み出され、発展していき、 最近ではファイナンスにおいても使用されています。 特にここでは ランダムな連関とリーマンショックなどの大事件(ノイズ)をフィルターにかけて排除し、 純粋な相互連関を突き止めることを行っています。
半円則
要素が独立, 平均 0, 分散が 1/2
# 行列を作成
> size<-100;
> m<-array(0,c(size,size));
> for(i in 1:size) {
+ for(j in 1:size) {
+ m[i,j]<-rnorm(mean=0.0,sd=0.5,n=1);
+ m[j,i]<-m[i,j];
+ }
+ }
> print(m);
略
# 固有値を計算する
> ev<-eigen(m);
> print(ev$values);
略
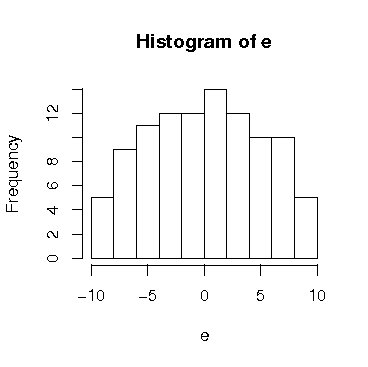
> e<-ev$values;
> hist(e);
|
円則
1000次元の正方行列を考えて各要素は独立に標準正規分布に従うとします。 こうしてできる行列は実非対称な行列になります。
> A=matrix(rnorm(1000000),nc=1000)
> Eigen=eigen(A)
> plot(Eigen$value,xlab="Re",ylab="Im")
> title("Eigen value of real\nonsymmetric 1000x1000 matrix")
|

円状に固有値が分布しており、Gilikoの円則と呼ばれている。
【参考文献】
理論に関しては:
応用に関しては:
Back to R