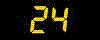R-Regression

回帰分析を行なうために以下の関数が用意されている．

lsfit() ：最小二乗法による回帰を行う．

lm() ：線形モデルによる回帰を行う

glm() ：一般線形モデルによる回帰を行う

単回帰分析・直線回帰

関数 lm() と predict() を用いて単回帰分析を行うことができる．

ここで対象となるモデルは以下のような線形モデルである．

$y_i=\displaystyle\sum_{j=0}^{k}\beta_{j}x_{ij} \epsilon_i,\epsilon_i\sim(0,\sigma^2),i=1,\cdots,n$

上式をベクトル表記すると y = Xb + e となる．このときの y は応答ベクトル，X は説明変数のベクトル（モデル行列）で，x₀ は切片項（要素が全て 1 である列ベクトル）となっている．

　例えばデフォルトで入っている以下のようなアメリカ桜のデータtrees があったとする．このデータに関して散布図を描いた後，単回帰分析を行う．

Girth ：木の直径（数値，単位はインチ）

Height ：木の高さ(数値，単位はフィート）

Volume ：長さ 1 フィートの立方体に切ったときの重さ

 
 plot(Volume ~ Girth, data = trees)                           # 散布図を描く 
 result <- lm(Volume ~ Girth, data = trees)                   # 回帰分析を行う 
 abline(result)                                               # 推定回帰直線を描く 
 summary(result)                                              # 分析結果の要約 
 
Call:
lm(formula = Volume ~ Girth, data = trees)
Residuals:
    Min      1Q  Median      3Q     Max 
-8.0654 -3.1067  0.1520  3.4948  9.5868 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -36.9435     3.3651  -10.98 7.62e-12 ***
Girth         5.0659     0.2474   20.48  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
Residual standard error: 4.252 on 29 degrees of freedom
Multiple R-Squared: 0.9353,     Adjusted R-squared: 0.9331 
F-statistic: 419.4 on 1 and 29 DF,  p-value: < 2.2e-16

結果は -36.9435 が切片項，5.0659 が傾きの推定値となっている．ここで，予測区間と信頼区間をプロットしてみる．

 
 new <- data.frame(Girth = seq(8, 24, 0.5))
 result.pre <- predict(result, new, interval="prediction")    # 予測区間 
 result.con <- predict(result, new, interval="confidence")    # 信頼区間 
 matplot(new$Girth, cbind(result.pre, result.con), lty=c(1,2,2,3,3), type="l")

プロット結果は以下のようになる．

関数 lm() で回帰分析を行った要約結果を変数 result に代入した場合，result$fstatistic は実際の F 検定結果と自由度は返すが p 値は返さない．自力で F 統計量の p 値を計算する場合は以下のようにすればよい．

 
 result <- summary( result <- lm(Volume ~ Girth, data = trees) )
 f.stat <- result$fstatistic
 p.value <- 1-pf(f.stat["value"],f.stat["numdf"],f.stat["dendf"])
 p.value
 
value 
    0

両対数を取ってから線形回帰モデルの当てはめを行うこともできる．

 
 result1 <- lm(log(Volume) ~ log(Girth), data = trees)
 summary(result1)

関数 lm() の書式と引数

書式は以下の通りである．重要なのはモデルを指定する引数 formula と，データ名を指定する引数 data である．

 
 lm(formula, data, subset, weights, na.action,
    method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
    singular.ok = TRUE, contrasts = NULL, offset = NULL, ...)

引数 formula と回帰のモデル式の対応表を挙げる．

formula	回帰におけるモデル式
y ~ x	モデル式 y = a + bx + ε（ ε は誤差項）について，目的変数 y と説明変数 x をベクトルで指定する．
y ~ x1 + x2	モデル式 y = a + b₁x₁ + b₂x₂ + ε（ ε は誤差項）について，目的変数 y と説明変数 x₁，x₂ をベクトルで指定する．
*y ~ x1 x2**	交互作用項を含んだモデル式（ x1:x2 でもよい） y = a + b₁x₁ + b₂x₂ + b₃x₁x₂ + ε（ ε は誤差項）について，目的変数 y と説明変数 x₁，x₂ をベクトルで指定する．
*y ~ x1 + x2 + x1x2**	上と同じ交互作用モデル．
y ~ (x1 + x2)^2	上と同じ交互作用モデル．
y ~ x - 1	切片(定数)項を除外する（ + 0 でも可）．
y ~ 1 + x + I(x^2)	多項式回帰： y = b₀ + b₁x₁ + b₂x² + ε（ ε は誤差項）．I(x^2) は poly(x,2) でも可．
y ~ x \| z	z で条件付けしたときの y の x への単回帰．
y ~ . , data = データ名	あるデータに目的変数 y と説明変数 x₁，・・・が入っている場合で，モデル式がy = a + b₁x₁ + ・・・ + ε（ ε は誤差項）である場合は，まず，目的変数 y をベクトルで指定し，右辺は「 y 以外」という意味で . （ピリオド）を指定することも出来る．

モデル情報を取り出す関数

lm() の返り値は当てはめられたモデルのオブジェクトとなっている．このオブジェクト obj を以下の関数に与えることで，新たな統計処理を行うことが出来る．この中からよく使うものを説明する．

関数	機能
AIC(obj)	AIC（赤池情報量規準）を求める．
anova(obj1 , obj2)	モデルを比較して分散分析表を生成する．
coefficients(obj)	回帰係数 (行列) を抽出．coef(obj) と省略できる．
deviance(obj)	重みつけられた残差平方和．
formula(obj)	モデル式を抽出．
logLik(obj)	対数尤度を求める．
plot(obj)	残差，当てはめ値などの 4 種類のプロットを生成．
predict(obj, newdata=data.frame)	提供されるデータフレームが元のものと同じラベルを持つことを強制する．値は data.frame 中の非ランダムな変量に対する予測値のベクトルまたは行列となる．
print(obj)	オブジェクトの簡略版を表示．
residuals(obj)	適当に重みつけられた残差 (の行列) を抽出する．resid(obj) と省略できる．df.residuals(obj) も参照されたい．
step(obj)	階層を保ちながら，項を加えたり減らしたりして適当なモデルを選ぶ．この探索で見つかった最大の AIC (赤池情報量規準) を持つモデルが返される．
summary(obj)	回帰分析の完全な要約が表示される．

関数 anova() で分散分析表を書くことが出来る．

 
 anova(result1)
 
Analysis of Variance Table
Response: log(Volume)
           Df Sum Sq Mean Sq F value    Pr(>F)    
log(Girth)  1 7.9254  7.9254  599.72 < 2.2e-16 ***
Residuals  29 0.3832  0.0132                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1  
 
 aov(result1)
 
Call:
   aov(formula = result1)
Terms:
                log(Girth) Residuals
Sum of Squares    7.925446  0.383244
Deg. of Freedom          1        29
Residual standard error: 0.1149578 
Estimated effects may be unbalanced

以下はモデルの情報を取り出す一つの例である．以下は，result1 で使ったモデルに，さらに説明変数 log(Height) を取り入れて新たなモデルの当てはめを行っている．説明項に多少の変更を加えた場合でモデルの当てはめをやり直す場合には，この関数 update() を用いるのが便利である．

 
 result1 <- lm(log(Volume) ~ log(Girth), data = trees)
 result2 <- update(result1, ~ . + log(Height), data = trees)
 summary(result2)
 
Call:
lm(formula = log(Volume) ~ log(Girth) + log(Height), data = trees)
Residuals:
      Min        1Q    Median        3Q       Max 
-0.168561 -0.048488  0.002431  0.063637  0.129223 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -6.63162    0.79979  -8.292 5.06e-09 ***
log(Girth)   1.98265    0.07501  26.432  < 2e-16 ***
log(Height)  1.11712    0.20444   5.464 7.81e-06 ***

関数 step() を用いて，result2 のモデルについて，モデルから変数を 1 つ削った場合と変数を削らない場合の解析を全通り行い，各結果の AIC を比較している．

 
 result3 <- step(result2)
 
Start:  AIC= -152.69 
 log(Volume) ~ log(Girth) + log(Height) 
 
              Df Sum of Sq      RSS      AIC
<none>                        0.185 -152.685
- log(Height)  1     0.198    0.383 -132.185
- log(Girth)   1     4.628    4.813  -53.743 
 
 summary(result3)
 
Call:
lm(formula = log(Volume) ~ log(Girth) + log(Height), data = trees)
Residuals:
      Min        1Q    Median        3Q       Max 
-0.168561 -0.048488  0.002431  0.063637  0.129223 
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -6.63162    0.79979  -8.292 5.06e-09 ***
log(Girth)   1.98265    0.07501  26.432  < 2e-16 ***
log(Height)  1.11712    0.20444   5.464 7.81e-06 ***

説明変数に非説明変数以外の全てを指定する場合は .（ピリオド）を指定し，切片項を取り除く場合は$-1$を指定する．

 
 result <- lm(log(Volume) ~ .-1, data = trees)
 summary(result)
 
Call:
lm(formula = log(Volume) ~ . - 1, data = trees)
Residuals:
      Min        1Q    Median        3Q       Max 
-0.188133 -0.072707 -0.001769  0.062948  0.174312 
Coefficients:
       Estimate Std. Error t value Pr(>|t|)    
Girth  0.144695   0.006381   22.68  < 2e-16 ***
Height 0.017830   0.001138   15.66 1.09e-15 ***

関数 lsfit() による最小二乗法

関数 lsfit() により，y = X b + e の b を推定する．y には従属変数（被説明変数）のベクトルを与え，X には独立変数（計画行列，説明変数；それぞれがベクトル）を cbind したものを与える．つまり，この行列の各列が説明変量で各列が観測値となる．lsfit() の書式は以下の通り．

 
 lsfit(x, y, wt=NULL, intercept=TRUE, tolerance=1e-07, yname=NULL)

引数の説明は以下の通り．

引数	機能
x	説明変数の行列．
y	被説明変数のベクトル．
wt	重みをつける場合はここに指定する．
intercept	デフォルトは TRUE で，この場合は自動的に計画行列（説明変数の行列）に定数項が加わる．定数項を加えたくない場合は FALSE を指定する．

例として，データ trees に関して最小二乗法を行う．

 
 x <- trees$Height;  y <- trees$Volume
 z <- lsfit(x, y)      # 推定結果を z に格納 
 print(z)              # coefficients, residuals, intercept, qr を出力

出力の説明は以下の通り．

引数	機能
coef	回帰係数ベクトル．intercept=T (デフォルト) ならば第 1 要素が回帰式の定数項とる．
residuals	残差ベクトル．
intercept	引数interceptと同じ値で，説明行列が定数項に対応する列を含んでいるか否かを示す．
qr	x に定数項に対応する列を追加した行列を QR分解した結果．この要素の副要素 qt は t(Q) %*% y を表し ( t(Q) は Q の転置行列) ，この要素の qt 以外の副要素は関数 qr が返す要素をそのまま保持している．

回帰による予測値を求める場合は，出力 z について以下の様に入力すればよい．

 
 y - z$residuals
 
 [1] 20.91087 13.19412 10.10742 23.99757 37.88772 40.97442 14.73747 28.62762
 [9] 36.34437 28.62762 34.80102 30.17097 30.17097 19.36752 28.62762 27.08427
[17] 44.06112 45.60447 22.45422 11.65077 33.25767 36.34437 27.08427 23.99757
[25] 31.71432 37.88772 39.43107 36.34437 36.34437 36.34437 47.14782

関数 ls.diag(z) で残差の標準偏差やハット行列 H の対角成分などが得られる．

また，重相関係数 R = (予測値の分散) / (被説明変数の分散) を求める場合には以下の様に入力すればよい．

 
 sqrt(var(y - z$residuals)/var(y)) 
 
[1] 0.5982497

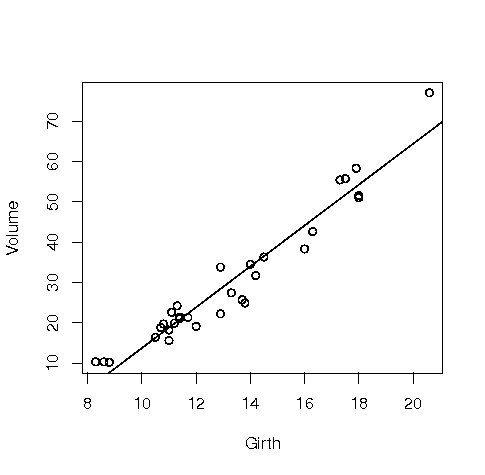
以下のように lsfit() の結果を abline() に渡すことによって，回帰直線を描くことも出来る．

 
 plot(x, y)
 abline(z, col=2)

一般化線形モデル

関数 glm() を用いることで一般化線形モデルを扱うことが出来る．

一般化線形モデルのクラスは，応答変数の分布が正規分布（gaussian），二項分布（binomial），ポアソン分布（poisson），逆正規分布（inverse.gaussian），ガンマ分布（Gamma），そして応答分布がはっきりしないときのための擬似尤度モデル（quasi）を備えており，引数 family で指定することが出来る．ファミリー名とリンク関数の表を以下に挙げる．

引数 family	リンク関数
binomial	logit, probit, log, cloglog
gaussian	identity, log, inverse
Gamma	identity, inverse, log
inverse.gaussian	1/mu^2, identity, inverse, log
poisson	identity, log, sqrt
quasi	logit, probit, cloglog, identity, inverse, log, 1/mu^2, sqrt

ロジスティックモデル $p(x)=\frac{1}{1 \exp\{-(\beta_0 \beta_1x)\}}$ の例を挙げる．

 
 b0 <- -3;    b1 <- 0.5;    x <- seq(0, 10, 0.1)
 p  <- 1/(1+exp(-b0+b1*x))
 mydata <- rbinom(length(x), 1, prob=p)
 result <- glm(mydata ~ 1+x, binomial(logit))
 summary(result)
 
Call:
glm(formula = mydata ~ 1 + x, family = binomial(logit))
Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-0.28951  -0.16852  -0.09972  -0.05892   2.86202  
Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  -3.1513     1.4901  -2.115   0.0344 *
x            -0.4216     0.4925  -0.856   0.3919

非線形回帰分析

関数 nls() を用いることによって非線形回帰分析を行うことが出来る．

 
 f <- function(x) 1/(1+exp(-3-0.5*x))
 x <- seq(0,10,0.1);   y <- f(jitter(x, amount=0.2))
 ( result <- nls(y ~ a/(1+exp(-b-c*x)), start=c(a=2,b=1,c=0.1)) )
 
Nonlinear regression model
  model:  y ~ a/(1 + exp(-b - c * x)) 
   data:  parent.frame() 
        a         b         c 
1.0000121 3.0203203 0.4931959

非線形混合モデルはパッケージ nlme 中の関数 nlme() で実行できる．

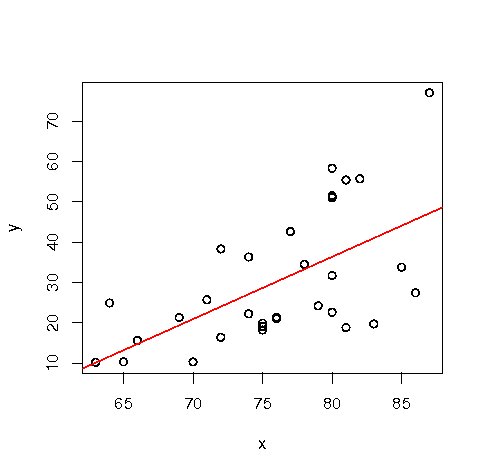
データに対して当てはめ曲線を描くことも出来る．

 
 predict.c <- predict(result)
 plot(x, y, ann=F, xlim=c(0,10), ylim=c(0.95,1));   par(new=T)
 plot(x, predict.c, type="l", xlim=c(0,10), ylim=c(0.95,1),col="red")

Back to R