1.基本概念
(1) 生存時間分析
生存時間分析(survival analysis)はイベント(event)が起きるまでの時間とイベントとの間の関係に焦点を当てる分析方法である。 生存時間分析は経済学では失業者が再就職する過程、金融工学においては倒産モデル、 工学分野においては機械システムや製品の故障などを、医学分野においては疾患の病気の再発や死亡などを対象とした研究分野である。 このような故障、破壊、倒産、再発、死亡などのイベントの生起のことを広義で死亡と呼ぶことにする。 このモデルはロジットモデルと同様の関数形であるが、 デフォルト・死亡の可能性を考慮に入れたものである。
(2) 打ち切り
生存時間に関する試験・観察を行うとき、治療の中止、もしくは転院、試験・観察の途中で脱落する場合がある。 また研究の終了時点では死亡に関するデータが入手できないことが起り得る。 このようなことを打ち切りが生じた(censoring)と言う。 打ち切りは左側打ち切り、右側打ち切りなどに分類する場合があるが、 ここでは研究を終了するまでイベントが観測できなかったケースを打ち切りと呼ぶことにする。
Rの生存時間分析のパッケージとして最も広く用いられているのはsurvivalである。 パッケージsurvivalは自動的にインストールされており、 またパッケージMASSにはgehanという生存時間データがある。 データgehan は白血病患者に対する薬の効果を調べるために被験者42名に対して行った臨床試験データである。 被験者は薬の投与群と対照群(投薬していない群)のペアによって構成されている。 生存時間データの形式および打ち切りに関する情報を確するためデータフレームgehanの構造を次に示す。 また同様の医療データとして、amlがあるが これは急性骨隋白血病のデータである。
> library(survival); > library(MASS); > data(gehan); > gehan[1:6,] pair time cens treat 1 1 1 1 control 2 1 10 1 6-MP 3 2 22 1 control 4 2 7 1 6-MP 5 3 3 1 control 6 3 32 0 6-MP |
変数pairは投薬と比較対象のペア、timeは生存時間、censは打ち切りか否か(0,1)、treatは6-MP薬の投与か否かである。
パッケージsurvivalには生存時間データオブジェクトを作成する関数Survがあり、返された結果は通常生存時間モデルの目的変数(あるいは被説明変数)として用いられる。
次に関数Survを用いた例を示す。返される結果の値の右側に記号+が付いている値は打ち切りデータである。
> Surv(gehan$time,gehan$cens) [1] 1 10 22 7 3 32+ 12 23 8 22 17 6 2 16 11 34+ 8 32+ [19] 12 25+ 2 11+ 5 20+ 4 19+ 15 6 8 17+ 23 35+ 5 6 11 13 [37] 4 9+ 1 6+ 8 10+ |
図1に横軸を生存時間としたデータgehanの棒グラフを示す。 棒の右側の×印は、研究が終了する前に死亡が確認されたもので、△印は研究が終了する前に何らかの理由で観測が継続できなかった打ち切りであり、○印は研究が終了する時点まで生存した打ち切りである。 打ち切りがあるデータを不完全データ、打ち切りがないデータを完全データと呼ぶ。
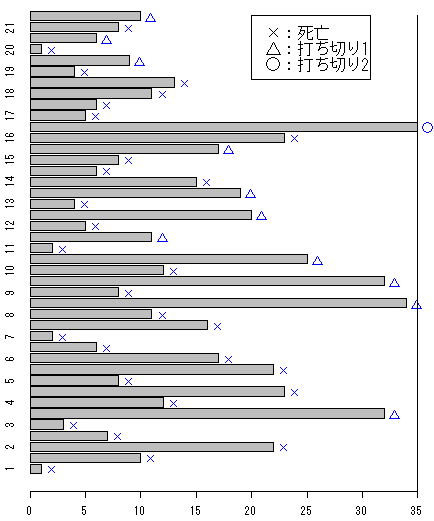
図1 生存時間の横棒グラフ
(3) 生存関数とハザード関数
生存時間Tを確率変数、確率密度関数を次のように表す。
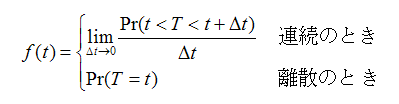
累積確率分布関数をF(t)で表すと、イベントがある時点tまで生起していない生存関数S(t)(survival function)を次のように表す。
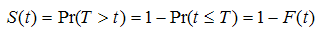
イベントがある時点t までに生起していないという条件の下で,次の瞬間にイベントが生起する瞬間死亡率を示すハザード関数h(t)(hazard function)は次のようになる。
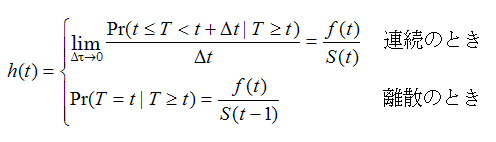
ハザードは危険度とも呼ばれている。 生存関数S(t)とハザード関数h(t)および累積ハザード関数H(t)との関係は次のように表すことができる。
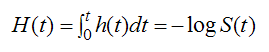
(4) 生存時間分析の分類
生存時間分析は生存時間に影響を与える時間以外の共変量(複数の要因、説明変数)がパラメータとして作成するモデルに導入されているか否か,生存時間の分布形に特定の確率分布を仮定するか否かによって、次のように分類することができる。
◇ノンパラメトリックモデル(non-parametric model 、共変量を導入しない、分布を仮定しない)
◇セミノンパラメトリックモデル(semi-non-parametric model、共変量を導入する、分布を仮定しない)
◇パラメトリックモデル(parametric model 、共変量を導入する、分布を仮定する)
2.ノンパラメトリックモデル
(1) ノンパラメトリックの推定法
ノンパラメトリックの推定方法とは、確率分布を仮定せずに生存時間を推定する方法で、経験分布による推定法とハザード関数による推定法がある。
i) 経験分布による推定法
打ち切りがない完全データであれば、収集したデータに基づいた累積分布関数、つまり経験分布関数F(t)を用いて推定することができる。
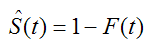
これは後述のカプラン・マイヤー(Kaplan Meier)推定法の特殊なケースである。 カプラン・マイヤー推定法は、条件付き確率の考え方に基づき、次のように定義される。
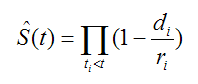
式の中のdiは、時点tiの死亡数、riは時点tiの直前までイベントが生じる可能性のある観察対象者の数(リスクセット)である。
ii) ハザード関数による推定法
カプラン・マイヤー推定量を用いて累積ハザード関数を推定することができる。 累積ハザード関数およびその推定量はそれぞれ
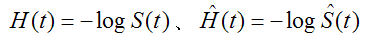
カプラン・マイヤー推定量から求めたハザードの推定量
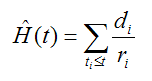
をネルソン(Nelson)推定量、あるいはネルソン・アーラン(Nelson-Aalen)推定量と呼ぶ。 これは小サンプルに有効であると言われている。ネルソン推定量を修正した
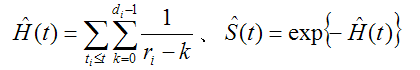
をフレミング・ハリントン(Fleming-Harrington)推定量と呼ぶ。
(2) 関数survfit
パッケージsurvivalにはノンパラメトリック法による生存時間を当てはめる関数survfitがある。 関数survfitは引数typeを用いて推定法を指定する。 関数survfitには3種類の推定方法が用意されている。 デフォルトに設定されているカプラン・マイヤー推定法(Kaplan−Meier)のほかにFleming−Harrington推定法、fh2推定法がある。関数survfitの書き式を次に示す。
survfit(formula, data,type=" ",…)
引数formulaでは次に示す例のようにSurvオブジェクト形式の目的変数と説明変数を指定する。 次にデータgehanの生存時間timeを目的変数、投薬したか否かのデータを記録したtreat列を説明変数とした関数survfitの使用例を示す。 その他の引数はデフォルトの値を用いた。
> ge.sf<-survfit(Surv(time,cens)~treat,data=gehan)
> ge.sf
Call: survfit(formula = Surv(time, cens) ~ treat, data = gehan)
records n.max n.start events median 0.95LCL 0.95UCL
treat=6-MP 21 21 21 9 23 16 NA
treat=control 21 21 21 21 8 4 12
|
このように、データgehanにおける投薬群と対照群ごとの標本数、イベントの件数、中央値、両側の区間推定に関する情報を返す。
関数summaryを用いると、各標本の生存時間time、リスクセットn.risk、イベントの数n.event、推定された生存確率survival、標準誤差std.err、95%信頼区間の上下限値を返す。
> summary(ge.sf)
Call: survfit(formula = Surv(time, cens) ~ treat, data = gehan)
treat=6-MP
time n.risk n.event survival std.err lower 95% CI upper 95% CI
6 21 3 0.857 0.0764 0.720 1.000
7 17 1 0.807 0.0869 0.653 0.996
10 15 1 0.753 0.0963 0.586 0.968
13 12 1 0.690 0.1068 0.510 0.935
16 11 1 0.627 0.1141 0.439 0.896
22 7 1 0.538 0.1282 0.337 0.858
23 6 1 0.448 0.1346 0.249 0.807
treat=control
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 21 2 0.9048 0.0641 0.78754 1.000
2 19 2 0.8095 0.0857 0.65785 0.996
3 17 1 0.7619 0.0929 0.59988 0.968
4 16 2 0.6667 0.1029 0.49268 0.902
5 14 2 0.5714 0.1080 0.39455 0.828
8 12 4 0.3810 0.1060 0.22085 0.657
11 8 2 0.2857 0.0986 0.14529 0.562
12 6 2 0.1905 0.0857 0.07887 0.460
15 4 1 0.1429 0.0764 0.05011 0.407
17 3 1 0.0952 0.0641 0.02549 0.356
22 2 1 0.0476 0.0465 0.00703 0.322
23 1 1 0.0000 NaN NA NA
|
次のように関数plotを用いると生存確率の推測値のプロットを返す。
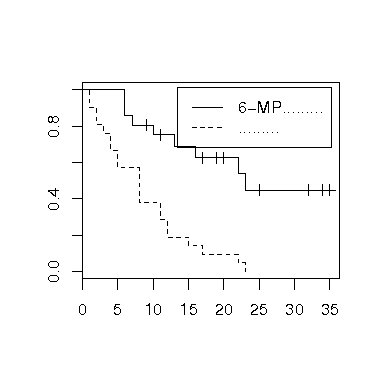
図2 データgehanの生存時間プロット
生存曲線プロットの折れ線に+印が付いているところは打ち切りがある時点である。 関数plotに引数mark.t=Fを用いると印+が除かれる。 また引数formulaで、打ち切りデータを省略することができる。 作図する時、引数conf.int=TRUEを加えると生存曲線プロットに信頼区間が表示される。 ただし生存曲線が1本である場合は、conf.int=TRUEを省略しても、信頼区間が作成される。
次にgehanの投薬群のみのデータについてカプラン・マイヤー法による生存曲線と90%の信頼区間を示す作図コマンドの例を示し、その結果を図3に示す。
> ge2<-subset(gehan,treat="6-MP")
36 件の警告がありました (警告を見るには warnings() を使って下さい)
> ge2.s<-survfit(Surv(time,cens)~treat,conf.int=.9,data=ge2)
> plot(ge2.s,mark.t=F)
> legend(locator(1),lty=c(1,2),legend=c("生存曲線","信頼区間"))
|
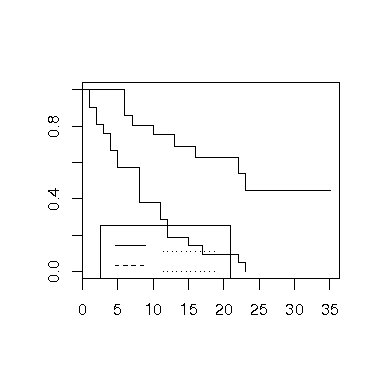
図3 生存曲線と信頼区間
カプラン・マイヤー推定量 は漸近的に正規分布に従うことが知られており、標準偏差は、次の式を用いて推定することができる。
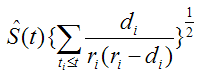
ネルソン推定量の標準偏差は次の式で求める。
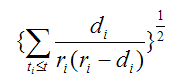
関数survfitには信頼区間を推定する方法を指定する引数conf.typeが用意されている。 引数conf.typeは、"none", "plain", "log", "log-log"の中から1つ選択できる。 デフォルトには"log"になっている。 "none"の場合は信頼区間を返さない。 それぞれのconf.typeは次の式で推測される。 式の中の
"plain":
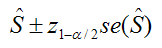
"log":
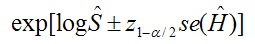
"log-lig":
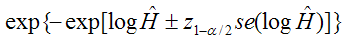
"plain"と"log"で求めた信頼区間の上限値は1を超える場合があるが、そのときには1を超える部分は切り捨てる。 "log-log"による計算結果は1以内に収まる。
データge2の3種類("plain", "log", "log-log")のconf.typeの信頼区間を求め、図示するコマンドの例を次に示し、その結果を図4に示す。
> plot(ge2.s,conf.int=TRUE,mark.t=F)
48 件の警告がありました (警告を見るには warnings() を使って下さい)
> lines(survfit(Surv(time,cens)~treat,data=ge2,conf.type="plain"),mark.t=F,conf.int=TRUE,lty=3,col=3)
> lines(survfit(Surv(time,cens)~treat,data=ge2,conf.type="log-log"),mark.t=F,conf.int=TRUE,lty=4,col=4)
> legend(locator(1),c("log","plain","log-log"), lty=c(1,3,4),col=c(1,3,4))
|
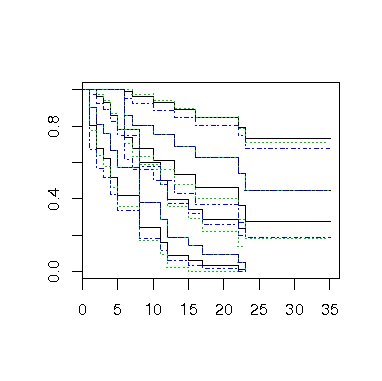
図4 異なる推定法による信頼区間
関数survfitには、信頼区間を指定する引数conf.intがあり、デフォルトはconf.int=.95になっている(95%の信頼区間)。引数conf.intの値は自由に指定することができる。
関数survfitにおける引数typeに fleming-harrington(fhに略することができる)あるいはfh2を指定するとフレミング・ハリントン推定量を返す。 異なる推定法の結果を考察する際に必要となる生存曲線のプロットを作成するコマンドの例を次に示し、その結果を図5に示す。
> ge2.s <-survfit(Surv(time,cens)~ treat, data= ge2)
> ge2.fh<-survfit(Surv(time,cens)~treat, data= ge2,type="fleming-harrington")
> ge2.fh2<- survfit(Surv(time,cens)~treat, data= ge2,type="fh2")
> plot(ge2.s,conf.int=F,mark.t=F)
> lines(ge2.fh,lty=2)
> lines(ge2.fh2,lty=3,col=2)
>legend(locator(1),lty=1:3,legend=c("Kaplan-meier","fleming-harrington","fh2"))
|
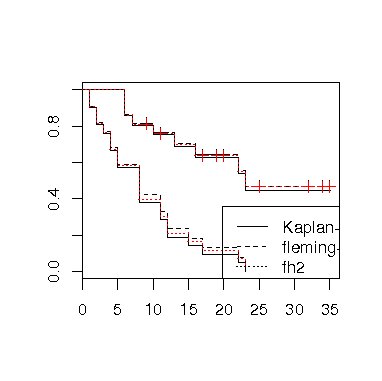
図5 3種類の推定法による生存曲線
(3) 生存関数の検定
データgehanのような2群(投薬群、対照群など)以上の観測値が得られたときには、群ごとの生存曲線の間の差の有意性について検定を必要とする場合がある。 最も広く用いられている検定方法はログ・ランク(log-rank)検定法である。 ログ・ランク(log-rank)検定法は、群ごとのイベントありとなしに集計したクロス表のカイ2乗検値の推定値を検定統計量とする。
> survdiff(Surv(time)~treat,data=gehan)
Call:
survdiff(formula = Surv(time) ~ treat, data = gehan)
N Observed Expected (O-E)^2/E (O-E)^2/V
treat=6-MP 21 21 29.2 2.31 8.97
treat=control 21 21 12.8 5.27 8.97
Chisq= 9 on 1 degrees of freedom, p= 0.00275
|
ログ・ランク検定のp値は約0.003であるので、仮に通常よく用いられている有意水準5%を規準とすると、両群(投薬群と対照群)の生存曲線には有意な差が認められる。
3.セミノンパラメトリックモデル
(1) コックス比例ハザードモデル
イベントに影響を及ぼす複数の因子(共変量)の影響を解析することを前提としたノンパラメトリックモデルをセミノンパラメトリックモデルと呼ぶ。最も広く用いられているモデルはコックス比例ハザードモデル(Cox proportional hazard model)である。
2つのハザード(瞬間死亡率)関数h1(t)、h2(t)が、すべて可能なt>0に対し、関係式h1(t)=ch2(t)が成り立つとき、2つのハザード関数は比例すると言う。 関係式の中のcは時間tと無関係な定数である。
共変量x=(x1,x2,…,xm)Tを持つハザード関数をh(t|x)とし、xを変数とする関数r(x)と、あるハザード関数h0がすべてのt>0とxについて関係式
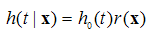
が成り立つとき、この式を比例ハザードモデル、あるいは比例危険度モデルと呼ぶ。
共変量xは、年齢や血圧のような連続変数、性別や結婚の有無のようなカテゴリカル変数、これらの交差項などを含む変数ベクトルである。
コックス比例ハザードモデルは、次の式で定義される。
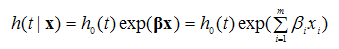
このモデルは、生存時間を目的変数とした回帰モデルである。共変量 がすべて0の場合のハザードをベースラインハザード(baseline hazard)と呼ぶ。コックス比例ハザードモデルは、ベースラインハザードを基準とした分析手法である。
モデルのパラメータβ=(β1,β2,…,βm) は、次に示す条件付きの確率の部分尤度(partial likelihood)を最大化する方法で推定できる
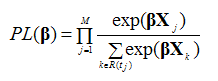
式の中のj=1,2,…,Mはイベントの数、tjはイベントの時点、R(tj)は各時点のリスクの集合である
(2) パラメータの推定
コックス比例ハザードモデルのパラメータの推定方法としては、直接法、Breslowの近似法、Efronの近似法などが提案されている。 直接法は、イベントの数が多くなると、部分尤度の分母の項が煩雑になるので、近似法としてBreslowの近似法、Efronの近似法が提案されている。 これらの近似法は、直接法と比較して計算が簡単であるが、同時に起こるイベントの数が多くなった場合、推定されるβが0に偏った値を取り、妥当性を失うと言われている。
パッケージsurvivalには、コックス比例ハザードモデルのパラメータを推定する関数coxphがある。関数 coxphの書き式を次に示す。
coxph(formula, data, method,…)
引数formulaには、モデルに用いる共変量などを指定する。 引数methodには、3種類(efron, breslow, exact)のオプションの中から1つを選択して指定する。 デフォルトは"efron"法が指定されている。
パッケージsurvivalの中に用意されているデータkidneyを用いた使用例を次に示す。データkidneyは、ポータブル透析装置の使用と腎臓患者の生存時間に関して、38ペア(使用と不使用)に対する実験データである。データセットの中の変数を次に示す。
| patient | ID |
| time | 時間 |
| status | 打ち切りは0、その他は1 |
| age | 年齢 |
| sex | 男性=1、女性=2 |
| disease | 病気の種類(GN,AN,PKD,Other) |
| frail | オリジナル論文からのフレイルティ(frailty)の推定値 |
データの中の性別(sex)と病気の種類(disease)を説明変数としたコックス比例ハザードモデルの解析例を次に示す。
> library(survival)
> data(kidney)
> kidney.cox<-coxph(Surv(time,status)~sex+disease,data=kidney)
> summary(kidney.cox)
Call:
coxph(formula = Surv(time, status) ~ sex + disease, data = kidney)
n= 76, number of events= 58
coef exp(coef) se(coef) z Pr(>|z|)
sex -1.4774 0.2282 0.3569 -4.140 3.48e-05 ***
diseaseGN 0.1392 1.1494 0.3635 0.383 0.7017
diseaseAN 0.4132 1.5116 0.3360 1.230 0.2188
diseasePKD -1.3671 0.2549 0.5889 -2.321 0.0203 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.2282 4.3815 0.11339 0.4594
diseaseGN 1.1494 0.8700 0.56368 2.3437
diseaseAN 1.5116 0.6616 0.78245 2.9202
diseasePKD 0.2549 3.9238 0.08035 0.8084
Rsquare= 0.206 (max possible= 0.993 )
Likelihood ratio test= 17.56 on 4 df, p=0.001501
Wald test = 19.77 on 4 df, p=0.0005533
Score (logrank) test = 19.97 on 4 df, p=0.0005069
|
関数coxphは、変数ごとの係数β、exp(β)、係数の標準誤差、z値、p値、信頼区間、仮説H0=0,H1≠0の検定統計量などを返す。
関数coxphには3種類(尤度比の検定、ワルド検定、スコア検定)の検定が用いられている。 これらは、係数が正規分布に従う仮定の下で異なる角度から求めている。
モデルによる生存時間の当てはめは、次のように関数survfitを用いると便利である。
> kidney.fit<-survfit(kidney.cox)
> summary(kidney.fit)
Call: survfit(formula = kidney.cox)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
2 76 1 0.99018 0.00985 0.971059 1.000
7 71 2 0.96856 0.01831 0.933335 1.000
8 69 2 0.94641 0.02422 0.900102 0.995
9 65 1 0.93499 0.02685 0.883820 0.989
12 64 2 0.91106 0.03177 0.850869 0.976
13 62 1 0.89844 0.03411 0.834007 0.968
15 60 2 0.87273 0.03844 0.800550 0.951
16 58 1 0.85959 0.04046 0.783848 0.943
17 56 1 0.84591 0.04246 0.766654 0.933
22 55 1 0.83144 0.04446 0.748706 0.923
23 53 1 0.81625 0.04646 0.730084 0.913
24 52 1 0.80113 0.04830 0.711843 0.902
25 50 1 0.78592 0.05004 0.693710 0.890
26 48 1 0.76976 0.05184 0.674573 0.878
27 47 1 0.75369 0.05350 0.655802 0.866
28 46 1 0.73761 0.05503 0.637273 0.854
30 45 4 0.67000 0.06032 0.561621 0.799
34 41 1 0.65287 0.06137 0.543011 0.785
38 40 1 0.63574 0.06232 0.524602 0.770
39 39 1 0.61861 0.06317 0.506390 0.756
40 38 1 0.60147 0.06392 0.488373 0.741
43 37 1 0.58250 0.06463 0.468646 0.724
53 35 1 0.56288 0.06531 0.448382 0.707
58 33 1 0.54279 0.06594 0.427786 0.689
63 32 1 0.52270 0.06642 0.407467 0.671
66 31 1 0.50281 0.06677 0.387591 0.652
78 29 1 0.48209 0.06708 0.367010 0.633
96 28 1 0.46208 0.06717 0.347515 0.614
114 25 1 0.44051 0.06735 0.326443 0.594
119 24 1 0.41929 0.06734 0.306055 0.574
130 23 1 0.39842 0.06715 0.286338 0.554
132 22 1 0.37781 0.06678 0.267181 0.534
141 21 1 0.35745 0.06624 0.248591 0.514
152 19 2 0.31584 0.06486 0.211190 0.472
154 17 1 0.29608 0.06387 0.194001 0.452
156 16 1 0.27265 0.06289 0.173487 0.429
177 14 1 0.24811 0.06174 0.152353 0.404
185 13 1 0.22436 0.06018 0.132633 0.380
190 12 1 0.20143 0.05822 0.114311 0.355
196 11 1 0.17910 0.05588 0.097163 0.330
201 10 1 0.15675 0.05322 0.080583 0.305
245 9 1 0.13440 0.05018 0.064649 0.279
292 8 1 0.11323 0.04664 0.050506 0.254
318 7 1 0.09332 0.04259 0.038149 0.228
333 6 1 0.07474 0.03804 0.027567 0.203
402 5 1 0.05617 0.03300 0.017760 0.178
447 4 1 0.03948 0.02728 0.010191 0.153
511 3 1 0.02491 0.02093 0.004800 0.129
536 2 1 0.01224 0.01383 0.001336 0.112
562 1 1 0.00318 0.00613 0.000073 0.139
|
関数survfitで推定された生存曲線および信頼区間は、関数plotを用いて図示することができる。その例を次に示す。
> plot(kidney.fit) |
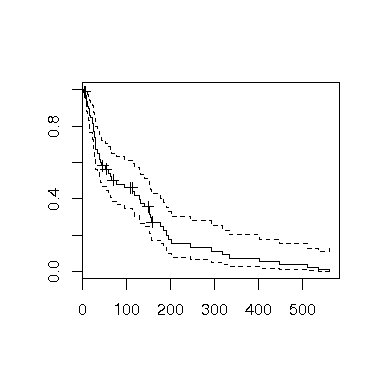
図6 推測されたkidney.fitの生存曲線
(3) 残差分析
生存分析のデータは打ち切りデータが含まれているので、残差分析は一般線形回帰モデルの残差分析ほど単純ではない。 そのためマルチンゲール残差(martingale residuals)、シェーンフィールド残差(Schoenfeld residuals)、スコア残差(score residuals)、デヴィアンス残差(deviance residuals)など幾つかの定義が提案されている。 それぞれ特徴を持っているのでどれが優れているかに関する評価はしがたいが、より多く用いられているのはマルチンゲール残差である。
coxphオブジェクトの残差は、関数residuals.coxph(略してresiduals)で求めることができる。 デフォルトには、マルチンゲール残差が指定されている。 関数residualsを使用する際には、短縮した文字列residを用いることも可能である。 既に求めたcoxphのオブジェクトkidney.coxの残差のプロットを、関数scatter.smoothを用いて作成する例を次に示す。
> scatter.smooth(residuals(kidney.cox)) > abline(h=0,lty=3,col=2) |
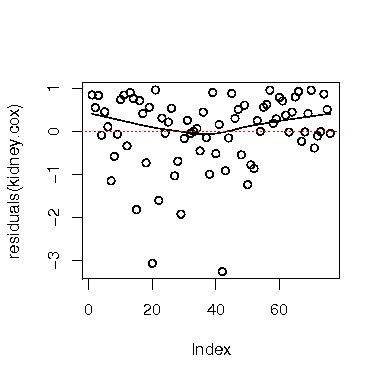
図7 マルチンゲール残差プロット
残差プロットから分かるように、マルチンゲール残差の最大値は1で、最小値は下限がない歪んだ分布である。 この歪んだ分布を標準化して扱いやすくするために考案されたのがデヴィアンス残差である。 デヴィアンス(尤離度)残差は、関数residualsに引数type="deviance"を用いることで、求めることができる。 その例を次に示す。
> scatter.smooth(residuals(kidney.cox,type="deviance")) > abline(h=0,lty=3,col=2) |
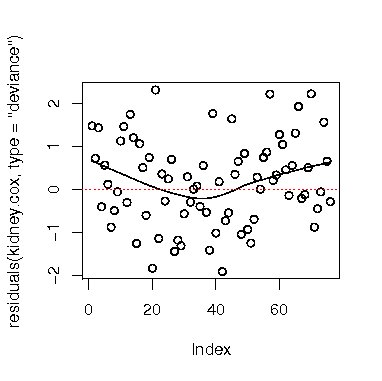
図8 デヴィアンス残差プロット
シェーンフィールド残差、スコア残差は関数residualsにそれぞれ引数type=" schoenfeld "、type=" score "を指定することで求めることができる。
(4) ハザードの比例性の分析
コックス比例ハザードモデルの前提はハザード比が時間によらず一定であることである。 よって、比例ハザードモデルを用いる場合は、この仮定を吟味する必要がある。
パッケージsurvivalには、比例性を分析する関数cox.zphが用意されている。 関数cox.zphはシェーンフィールド残差を用いて、β(t)=β+θg(t)における仮説H0:θ=0の検定に関する計算結果を返す。 式の中のg(t)は滑らかな関数である。また、関数cox.zphはg(ti)と標準化されたシェーンフィールド残差との相関係数をも返す。
関数cox.zphには引数transformがあり、式β(t)=β+θg(t)の中のg(t)を指定する。 デフォルトにはKaplan-Meier推定量
引数transformの関数g(t)をデフォルト値にし、kidney.coxを用いた例を次に示す。
> kidney.zph<-cox.zph(kidney.cox)
> kidney.zph
rho chisq p
sex 0.18839 2.60676 0.106
diseaseGN -0.01392 0.01123 0.916
diseaseAN 0.06162 0.20036 0.654
diseasePKD 0.00701 0.00438 0.947
GLOBAL NA 4.20781 0.379
|
仮説が棄却されると比例ハザードの仮定が充たされていない可能性があることを示唆する。ただし、仮説検定の結果はg(t)に依存することに留意してほしい。
関数plot.cox.zph (略してplot)を用いると変数ごとのシェーンフィールド残差プロットに、スプライン平滑(関数はsmooth.spline)化された曲線と標準誤差の2倍の信頼区間が示されるグラフを作成することができる。 スプライン平滑化の自由度は引数df="n"で指定できる。 デフォルトは、n=4になっている。
オブジェクトkidney.coxを用いた例を次に示し、その結果を図9に示す。 図9の各図はシェーンフィールド残差の各成分のプロットで、横軸は時間である。 ここでは、スプライン平滑化曲線の傾向を観察しやすくするため自由度df=2にした。
> par(mfrow=c(2,2)) > plot(kidney.zph,df=2) |
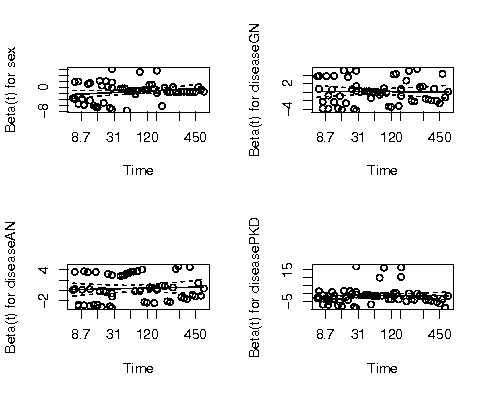
図9 比例性の診断プロット
スプライン平滑化曲線の傾向に、時間に伴う明らかな変化パターンが見られなければ比例ハザードの仮定には問題がないと言われている。 個別の変数に比例ハザードの仮定が充たされていない場合は、変数の交差項をモデルに導入するような試みが必要であろう。
(5) 交互作用と変数の選択
一般回帰分析の場合と同じく、コックス比例ハザードモデルの場合でも、説明変数の交互作用効果を取り入れたモデルの構築が可能である。 次にその例を示す。
> kidney.cox2<-coxph(Surv(time,status)~(sex+age+disease)^2,data=kidney)
> kidney.cox2
Call:
coxph(formula = Surv(time, status) ~ (sex + age + disease)^2,
data = kidney)
coef exp(coef) se(coef) z p
sex -2.61315 7.33e-02 1.2103 -2.159 0.031
age 0.02107 1.02e+00 0.0753 0.280 0.780
diseaseGN -0.78464 4.56e-01 3.0411 -0.258 0.800
diseaseAN -1.88260 1.52e-01 2.5810 -0.729 0.470
diseasePKD -14.36706 5.76e-07 5.5948 -2.568 0.010
sex:age -0.00440 9.96e-01 0.0404 -0.109 0.910
sex:diseaseGN 0.99539 2.71e+00 1.3429 0.741 0.460
sex:diseaseAN 1.30085 3.67e+00 1.2232 1.063 0.290
sex:diseasePKD 3.70973 4.08e+01 1.6914 2.193 0.028
age:diseaseGN -0.02313 9.77e-01 0.0288 -0.803 0.420
age:diseaseAN -0.00338 9.97e-01 0.0300 -0.113 0.910
age:diseasePKD 0.13961 1.15e+00 0.1114 1.253 0.210
Likelihood ratio test=32.9 on 12 df, p=0.00102 n= 76, number of events= 58
|
返されたp値から分かるように、年齢(age)はモデルへの寄与度が低い。 このようなモデルの作成にあまり役に立たない変数を取り除く(役に立つ変数を選択する)方法として、AIC情報量を用いる関数stepAICを用いることが可能である。 関数stepAICは、パッケージMASSに含まれている。 関数stepAICの応用例として、求めたオブジェクトkidney.cox2を用いた例とその結果を次に示す。
> library(MASS)
> stepAIC(kidney.cox2)
Start: AIC=366.95
Surv(time, status) ~ (sex + age + disease)^2
Df AIC
- age:disease 3 362.99
- sex:age 1 364.96
|
このように機械的にAIC情報量に基づいて最適と判断された結果が返される。
4.パラメトリックモデル
生存時間が確率分布に従う仮定の下でモデルを構築したモデルをパラメトリックモデルと呼ぶ。 パラメトリックモデルは、生存時間の確率分布を仮定する制約条件があるので、応用範囲が限定される。 パラメトリックモデルは、コックス比例ハザードモデルと比べると計算速度が速いのが特徴であるが、今日のコンピュータでは、もはや大きい問題として取り上げる必要がないであろう。
生存時間モデルに多く使われる確率分布は、指数分布、ワイブル分布、対数正規分布、対数ロジスティック分布などである。 これらの分布の確率密度関数、生存関数、ハザード関数を表1に示す。
| 分布名称 | 関数 |
| 指数(exponential) | 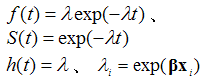 |
| ワイブル(weibull) | 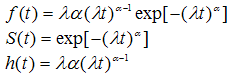 |
| 対数正規(log-normal) | 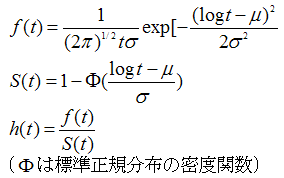 |
| 対数ロジスティック(log-logistic) | 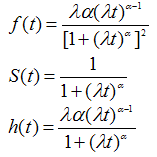 |
指数分布はワイブル分布の ときの特殊なケースである。
パッケージsurvivalには、パラメトリック生存モデルを当てはめる関数survregがある。 その書き式を次に示す。
survreg(formula=formula(data),dist="weibull", ...)
引数distで確率分布を指定する。 デフォルトにはワイブル分布が指定されている。 オプションとしては、指数分布(exponential)、ガウス分布(gaussian) 、対数正規分布 (log-normal) 、ロジスティック分布(logistic)、対数ロジスティック分布(log-logistic)が用意されている。
次に対数正規分布を用いた例を示す。
> survreg(Surv(time,status)~sex+disease,kidney,dis="lognormal")
Call:
survreg(formula = Surv(time, status) ~ sex + disease, data = kidney,
dist = "lognormal")
Coefficients:
(Intercept) sex diseaseGN diseaseAN diseasePKD
1.7923643 1.5062960 -0.3334601 -0.5321264 0.6810495
Scale= 1.129394
Loglik(model)= -329.1 Loglik(intercept only)= -340
Chisq= 21.8 on 4 degrees of freedom, p= 0.00022
n= 76
|
どの確率分布を用いた方がよいかに関しては、AICを用いて評価することができる。 関数survregは、直接AICを返さないが、対数尤度Loglike(model)を返すので、AIC求めることは困難ではない。
パッケージsurvivalには、生存分析に関する豊富なオブジェクトが用意されている。 日本語に訳された一覧表は次のサイトからパッケージ名前survivalで検索できる。
http://www.okada.jp.org/RWiki/index.php?cmd=search
【参考文献】
Back to R