1.基本概念
因子分析(factor analysis)は多くの変数により記述された量的データの分析方法である。 また因子分析で扱うデータの形式は主成分分析と基本的には同じであることから、同じ場面に利用されることが多い。 主成分分析では変数の間の相関関係を用いて、無相関の合成変数を求めることで多くの変数を少ない変数に縮約するが、因子分析は変数の間の相関関係から共通因子(common factor)を求めることで、多くの変数を少数個の共通因子にまとめて説明することを目的としている。 因子分析は観測データにおける変数の間の関連成分をまとめたものを共通因子と呼び、他の変数と関係がなく、その変数のみ持っている成分を独自因子(unique factor)と呼ぶ。 よって因子分析では観測データはお互いに関連性を持っており、共通因子と独自因子に分解できることを前提としている。
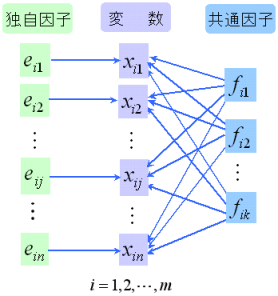
例: 表1のような観測データが図1に示すように 個の共通因子と独自因子により構成されたとすると、式1のようなモデルで表現できる。
| x1 | x2 | … | xj | … | xn | |
|---|---|---|---|---|---|---|
| 個体 1 | x11 | x12 | … | x1j | … | x1n |
| 個体 2 | x21 | x22 | … | x2j | … | x2n |
| … | … | … | … | … | … | … |
| 個体 i | xi1 | xi2 | … | xij | … | xin |
| … | … | … | … | … | … | … |
| 個体 m | xm1 | xm2 | … | xmj | … | xmn |
xi1=a11fi1+a12fi2+…+a1kfik+ei1
xi2=a21fi1+a22fi2+…+a2kfik+ei2
・・・
xij=aj1fi1+aj2fi2+…+ajkfik+eij (式1)
・・・
xin=an1fi1+an2fi2+…+ankfik+ein
i=1,2,・・・,m
xi2=a21fi1+a22fi2+…+a2kfik+ei2
・・・
xij=aj1fi1+aj2fi2+…+ajkfik+eij (式1)
・・・
xin=an1fi1+an2fi2+…+ankfik+ein
i=1,2,・・・,m
式の中のfikを共通因子fkの個体iの因子得点(factor score)と呼び、共通因子の係数を因子負荷量(factor loading)と呼ぶ。 表2に因子負荷量、表3にそれに対応する因子得点を示す。
| 因子負荷量 | ||||
|---|---|---|---|---|
| 第1 | 第2 | … | 第k | |
| xi1 | a11 | a12 | … | a1k |
| xi2 | a21 | a22 | … | a2k |
| … | … | … | … | … |
| xij | aj1 | aj2 | … | ajk |
| … | … | … | … | … |
| xn1 | an1 | an2 | … | ank |
| 因子得点 | ||||
|---|---|---|---|---|
| 第1 | 第2 | … | 第k | |
| 個体 1 | f11 | f12 | … | f1k |
| 個体 2 | f21 | f22 | … | f2k |
| … | … | … | … | … |
| 個体 i | fj1 | fj2 | … | fjk |
| … | … | … | … | … |
| 個体 m | fn1 | fn2 | … | fnk |
因子分析では式1からAn×k、Fn×kを求めるのが主な課題である。 式1の左側は観測・測定によって得られたデータで右側は共通因子と因子負荷量の線形結合に独自因子を加えている。 右側の各要素を求めることは比較的に複雑であり、何らかの条件の仮定が必要である。 異なる仮定のもとでいくつかのアルゴリズムが提案されている。 その中で最も広く用いられているのは主因子法(反復法)と最尤法である。 主因子法は安定した結果が得られるが、データが正規分布に従うときには最尤法を用いた方がよいと言われている。そのため異なるアルゴリズムから求められた結果を比較することは意味をなさない。
2.関数と使用例
最尤法による因子分析の関数factanalが実装されている。
factanal(x,factors,rotation,scores,…)
引数のxはデータセットで、factorsは求める因子の数である。因子の数は解析を行う際に指定しなければならない。主成分分析の結果から因子の数を決めると良い。 また引数rotationではバリマックス(varimax)回転とプロマックス(promax)回転を指定することができる。デフォールトには、直交回転“varimax”になっている。 そして引数scoresでは、因子得点を求める方法として、回帰方法(regression)とバートレット法(Bartlett)の中から1つ選択する。デフォールトには“none”になっているので、特別な方法を指定しないと、因子得点は求めない。 関数factanalが返す主な値として次がある。
$loadings 因子負荷量
$correlation 相関係数
$factors 求めた因子数
$STATISTIC カイ2乗値
$dof カイ2乗決定の自由度
$PVAL カイ2乗統計量のP値
バリマックス解
主成分分析と同様のデータを使用する。
> set.seed(123)
> x<-matrix(rnorm(100),ncol=5)
> colnames(x)<-paste("X",1:5,sep="")
|
相関係数行列は次のようになる (round関数により小数点以下3桁にそろえている)。
> round(cor(x),3)
X1 X2 X3 X4 X5
X1 1.000 -0.092 -0.125 0.122 -0.227
X2 -0.092 1.000 0.098 0.230 0.366
X3 -0.125 0.098 1.000 -0.148 -0.348
X4 0.122 0.230 -0.148 1.000 -0.126
X5 -0.227 0.366 -0.348 -0.126 1.000
|
このデータに対してバリマックス回転を行い、因子得点を求める。 抽出する因子数(factors引数)については解析結果の最後に示される因子数の十分正の検定結果や因子負荷量の2乗和が1以上になるものがないことを確認する必要がある。
> ans<-factanal(x,factors=2,scores="regression")
> ans
Call:
factanal(x = x, factors = 2, scores = "regression")
Uniquenesses:
X1 X2 X3 X4 X5
0.901 0.807 0.005 0.942 0.005
Loadings:
Factor1 Factor2
X1 -0.300
X2 0.436
X3 0.992 0.100
X4 -0.129 -0.203
X5 -0.441 0.895
Factor1 Factor2
SS loadings 1.208 1.132
Proportion Var 0.242 0.226
Cumulative Var 0.242 0.468
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 2.35 on 1 degree of freedom.
The p-value is 0.126
|
変数と因子の関係を把握するために次のような図を作成する。
plot(ans$loadings[,1],ans$loadings[,2],asp=1)
50 件以上の警告がありました (警告を見るには warnings() を使って下さい)
> abline(h=0,v=0)
> text(ans$loadings[,1],ans$loadings[,2],labels=paste("X",1:5,sep=""),pos=3)
|
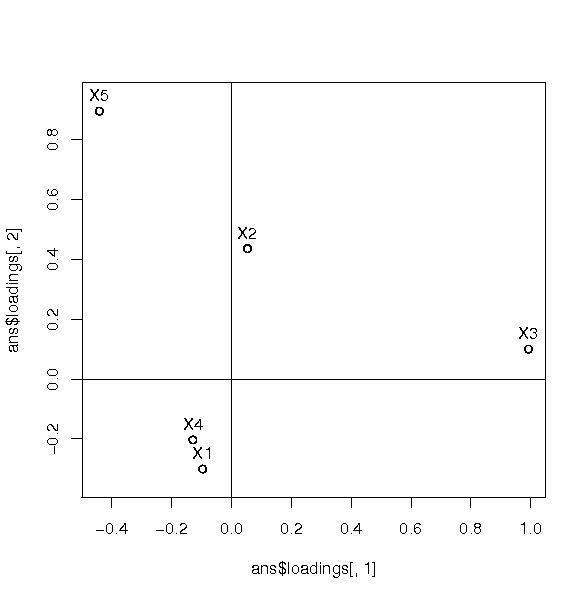
また因子得点はfactanal関数のscores引数で"regression"または"Bartleft"を指定した場合にはscoresという名前の要素に付値されるので、以下のようにして求められる。
> ans$scores
Factor1 Factor2
[1,] -0.75065366 -0.8636259
[2,] -0.31407240 -0.1392499
[3,] -1.27095852 -1.6242378
[4,] 2.01941095 1.3452687
[5,] 1.17651000 -0.2225578
[6,] -1.22395908 -0.6656475
[7,] -0.60271376 0.6726268
[8,] -0.57739306 -0.1984156
[9,] 0.76210891 -0.5687796
[10,] -0.29127423 0.8956500
[11,] 0.06434394 0.8584363
[12,] -0.15584741 0.1569120
[13,] -0.13081248 -0.2445360
[14,] 1.39235473 -0.6565770
[15,] -0.45892812 1.0989304
[16,] 1.53217440 -0.5574305
[17,] -1.88853490 1.5022855
[18,] 0.32655534 1.7126546
[19,] 0.09688342 -0.7717777
[20,] 0.29480594 -1.7299290
|
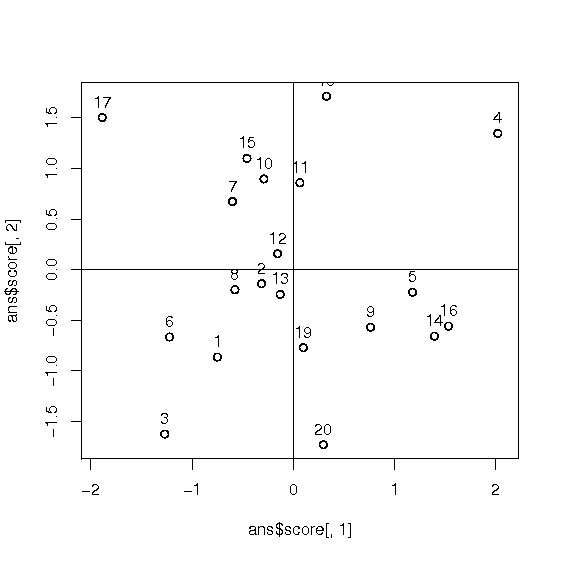
因子得点についても以下のように2つの因子の組み合わせで図を作成すると良い。
> plot(ans$score[,1],ans$score[,2],asp=1) > abline(h=0,v=0) > text(ans$score[,1],ans$score[,2],labels=1:20,pos=3) |
プロマックス解
バリマックス解は因子軸が直行するが、 因子軸が直行するということは因子間の相関がないことを意味する。 これに対して因子軸が直行しない(斜交する)とする因子分析もある。
> ans2<-factanal(x,factors=2,rotation="promax")
> print(ans2,sort=TRUE,cutoff=0)
Call:
factanal(x = x, factors = 2, rotation = "promax")
Uniquenesses:
X1 X2 X3 X4 X5
0.901 0.807 0.005 0.942 0.005
Loadings:
Factor1 Factor2
X5 0.982 -0.204
X3 -0.178 0.987
X1 -0.262 -0.168
X2 0.404 0.161
X4 -0.160 -0.175
Factor1 Factor2
SS loadings 1.254 1.100
Proportion Var 0.251 0.220
Cumulative Var 0.251 0.471
Factor Correlations:
Factor1 Factor2
Factor1 1.0000 0.0281
Factor2 0.0281 1.0000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 2.35 on 1 degree of freedom.
The p-value is 0.126
|
因果負荷量を全部書き出して(cutoff=0), 因果負荷量の順に並べる(sort=TURE)
> sort.loadings<-function(x)
+ {
+ y<-abs(x$loadings)
+ z<-apply(y,1,which.max)
+ lno<-NULL
+ s<-0
+ for(i in 1:ncol(y)){
+ t<-order(y[z==i,i],decreasing=TRUE)
+ lno<-c(lno,s+t)
+ s<-s+length(t)
+ }
+ loadings<-x$loadings[lno,]
+ class(loadings)<-"loadings"
+ return(loadings)
+ }
> print(sort.loadings(ans2),cutoff=0)
Loadings:
Factor1 Factor2
X3 -0.178 0.987
X2 0.404 0.161
X1 -0.262 -0.168
X4 -0.160 -0.175
X5 0.982 -0.204
Factor1 Factor2
SS loadings 1.254 1.100
Proportion Var 0.251 0.220
Cumulative Var 0.251 0.471
|
因子間相関関数
プロマックス回転は斜交回転のため因子間に相関が0ではない。 因子間の相関係数行列はfactanal関数では直接求めることができないため、 次のような関数を定義すると良い。
> factor.correlation<-function(x,factors)
+ {
+ ans<-factanal(x,factors,rotation="none")
+ ans2<-promax(ans$loadings)
+ ans3<-ans2$rotmat
+ r<-solve(t(ans3) %*% ans3)
+ colnames(r)<-rownames(r)<-colnames(ans2$loadings)
+ return(list(loadings=ans2$loadings,r=r))
+ }
|
factor.correlation関数は、x引数にデータフレーム、factorsに抽出する因子数を指定して呼び出すことで、因子間相関係数行列とプロマックス解による因子負荷量行列を返す。
> factor.correlation(x,2)
$loadings
Loadings:
Factor1 Factor2
X1 0.168 -0.262
X2 -0.161 0.404
X3 -0.987 -0.178
X4 0.175 -0.160
X5 0.204 0.982
Factor1 Factor2
SS loadings 1.10 1.254
Proportion Var 0.22 0.251
Cumulative Var 0.22 0.471
$r
Factor1 Factor2
Factor1 1.00000000 -0.02814076
Factor2 -0.02814076 1.00000000
|
Back to R